Combining transformations
Does changing the order of transformations always/sometimes/never
produce the same transformation?
Problem
In this problem, we shall use four transformations, $I$, $R$, $S$ and $T$. Their effects are shown below.
Image
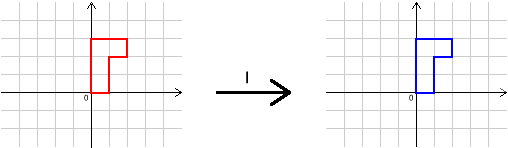
Image
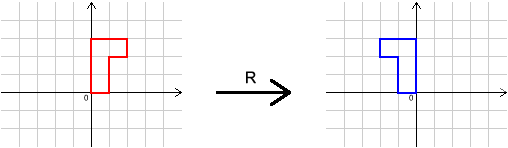
Image
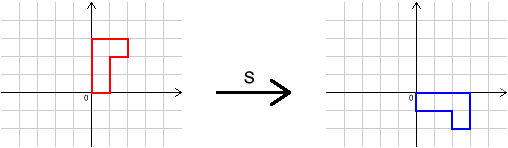
Image
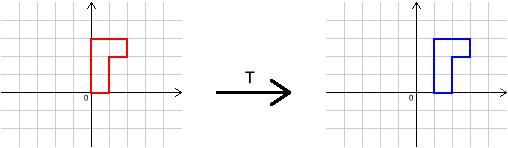
We write $R^{-1}$ for the transformation that ``undoes'' $R$ (the inverse of $R$), and $R S$ for "do $R$, then $S$".
We can write $T$ followed by $T$ as $T T$ or $T^2$, and $T$ followed by $T$ followed by $T$ as $T T T$ or $T^3$ and so on.
Similarly, we can write $S^{-1}S^{-1}$ as $S^{-2}$ and so on.
Try to find simpler ways to write:
$R^2$, $R^3$, $R^4$, $\dots$
$S^2$, $S^3$, $S^4$, $\dots$
$T^2$, $T^3$, $T^4$, $\dots$.
What do you notice?
Can you find a simpler way to write $R^{2006}$ and $S^{2006}$?
Can you describe $T^{2006}$?
Let's think about the order in which we carry out transformations:
What happens if you do $R S$? Do you think that $S R$ will be the same? Try it and see.
Is $T^2R$ the same as $R T^2$?
Is $(R T)S$ the same as $S(R T)$?
Try this with some other transformations.
Does changing the order always/sometimes/never produce the same transformation?
Now let's think about how to undo $R S$. What combination of $I$, $R$, $S$, $T$ and their inverses might work? Try it and see: does it work? If not, why not? Can you find a combination of transformations that does work?
How can you undo transformations like $S T$, $T R$ and $R S^2$?
This problem is the middle one of three related
problems.
The first problem is Decoding Transformations and the follow-up problem is Simplifying Transformations .
The first problem is Decoding Transformations and the follow-up problem is Simplifying Transformations .
Getting Started
If you need some squared paper you can download it here.
Hint for finding the inverse of $R S$:
If I put on my t-shirt and then put on my jumper, how can I undo this?
Which item of clothing do I have to take off first?
Student Solutions
Jannis from Long Bay showed he understood the effect of combining transformations. Well done Jannis.
$R^2=I$ (reflecting twice is the identity).
So $R^3=R$, $R^4=I$.
I noticed that if there is an even number of Rs the result is
the same as I. If there is an odd number of Rs the result is the
same as R.
$R^{2006}=I$ as 2006 is even.
$S$ is clockwise rotation by $90^{\circ}$ about the
origin.
So $S^2$ is clockwise rotation by $180^{\circ}$ about the
origin.
$S^3$ is rotation by $270^{\circ}$ clockwise about the origin
(the same as $S^{-1}$).
$S^4$ is rotation by $360^{\circ}$ about the origin (the same
as $I$).
So $S^{2006}=S^2$ as $S^{2000}=I$.
$T$ is translation one unit to the right;
$T^2$ is translation two units to the right;
$T^3$ is translation three units to the right, and so
on.
$T^{2006}$ is translation 2006 units to the right.
$R S$ is not the same as $S R$.
$R T^2$ is not the same as $T^2 R$.
$(R T)S$ is not the same as $S(R T)$.
However, changing the order does sometimes produce the same
transformation:
$R S^2=S^2 R$, for example.
The inverse of $R S$ is $(R S)^{-1}=S^{-1}R^{-1}$.
$(S T)^{-1}=T^{-1}S^{-1}$.
$(T R)^{-1}=R^{-1}T^{-1}$.
$(R S^2)^{-1}=S^{-2}R^{-1}$.
Teachers' Resources
This problem is the middle one of three related problems.
The first problem is Decoding Transformations and the follow-up problem is Simplifying Transformations .
We have adopted the convention of listing a sequence of transformations from left to right; teachers may want to mention to their students that in other contexts a sequence of transformations may be listed from right to left.
