LOGO challenge 12 - concentric circles
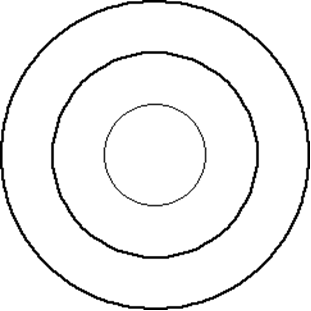
Can you reproduce the design comprising a series of concentric circles? Test your understanding of the realtionship betwwn the circumference and diameter of a circle.
Problem
Can you reproduce the following?
Image
Teachers' Resources
What is the relationship between the diameters of the circles?
What about the relationships between the circumferences?
The number of times the turtle turns and the distance it moves after each turn gives you the circumference which means you can calculate the diameter.
Where does the turtle need to be to start to draw each of the circles?
Instead of starting with the circumference - can you draw a circle with a known diameter?
