Spokes
Draw three equal line segments in a unit circle to divide the circle into four parts of equal area.
Problem
Image
|
Draw three equal line segments in a unit circle so that they
divide the disc into four parts of equal area.
What length do the line segments have to be? Generalise this result. |
Getting Started
Image
|
You know what the area of the four parts must be.
Think about symmetrical drawings.
Can you draw three lines inside the circle in such a way that
they enclose an area which can be expanded or contracted to give
the required area?
The Solution section gives one possibility (see link above).
There are many other possibilities you could investigate.
Here is just one alternative line of approach you could
pursue:
The diagram shows another solution for 3 lines but the same
principle applies to any regular polygon. For an $n$-gon the angle
marked at the centre of the circle $C$ will be ${\pi \over n}$. As
$n$ gets larger the polygons will get smaller and the lines will
'radiate' out more like the spokes of a wheel.
|
In general, if $L_n$ is the length of the spoke with $n$ spokes, $x_n$ the length of the edge of the polygon in the centre and $r_n$ the radius of the circumcircle of the polygon,then $$L_n = {x_n\over 2} + \sqrt {1 - (r_n\cos {\pi\over n})^2}$$ so that$L_n \to 1$ as $n\to \infty$.\par For $n=3$, $L_n \approx 1.595$; for $n=20$, $L_n\approx 1.011$ and for ${n=30}$, $L_n\approx 1.003$.
Student Solutions
There are many ways to solve this problem. See the Hints for suggestions of other lines of investigation you might like to pursue to find other solutions.
Andrei from Tudor Vianu National College, Bucharest, Romania has come up with an unexpected arrangement of the sticks. Here is Andrei's solution:
|
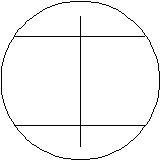
I chose to make $2$ segments of the unit, each of area a
quarter of the unit circle, and the remained part of the circle to
be divided into two equal parts, as shown in the figure.
Let $x$ be the central angle determined by the segment. The
area of the segment is: $${1\over 2}\left(x - \sin x\right).$$ And
it must be a quarter the area of the circle so: $${1\over 2}\left(x
- \sin x\right)= {\pi \over 4} .$$
|
Image
|
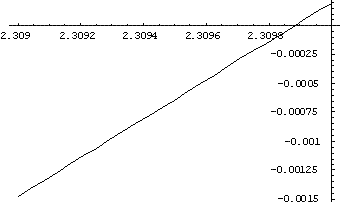
This equation could be solved only numerically, and to find an
approximate solution I represent the function $x-\sin x - {\pi
\over 2}$ and I look for a change of sign.
Image
|
To find a better approximation I used this graph.
Plot $\left[x - \sin [x]- {\pi \over 2}, {x, 2.309,
2.31}\right]$
So $x \approx 2.3099$.
|
Teachers' Resources
The challenge here is to visualise the diagram.
You can reason that a symmetrical solution is likely and then concentrate on the shape that is enclosed by the line segments. Calculate the angles and lengths in this shape before calculating the required lengths of the line segments.
You will need some trigonometry. Don't get put off by the calculation. The solution only requires simple geometry of right-angled triangles and polygons.
