Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Two Clocks



This problem could be worked on in a group of about four. For more details about how you might go about doing this, please read the Teachers' Notes.
Sam and Julie are friends. Both of them have rather odd clocks at home.
In Sam's bedroom there is an old alarm clock which his Dad had thrown out because it had lost its minute hand. Although it has only its small hand, Sam can still tell the time using it. He can tell the hour, such as midday. He can tell when it is time to get up, time to go to school and time to turn his light out at night.
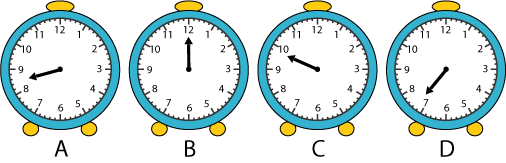
Which clock is showing it is midday?
At what time does Sam get up?
At what time does Sam go to school?
At what time is Sam supposed to turn out his light?
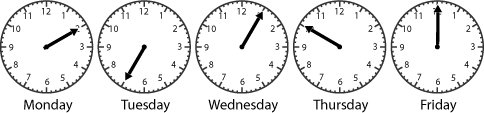
In Julie's hall there is a very old clock which lost its hour hand a long time ago.
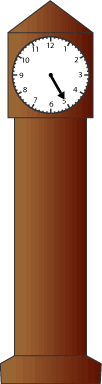
School finishes at half past three and it takes Julie at least half an hour to get home. Sometimes she goes to the shop on the way, and sometimes she leaves school a bit later. When she first gets home Julie always looks at the clock in the hall to see what time it is.
One week these were the times she saw: