Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Once Upon a Time
Age 7 to 11
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Once Upon a Time
Once upon a time there were three bears. There was Father Bear, Mother Bear and Baby Bear. But you knew that!
Mother Bear was three quarters the size of Father Bear.
Baby Bear was half the size of Father Bear.
And all the things they had were in the same proportions.
This means that Father Bear's chair was twice as big as Baby Bear's chair and Mother Bear's chair came exactly in between.
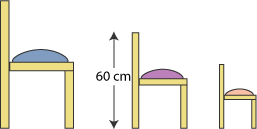
Mother Bear's chair was $60$ cm high. How high were the other two chairs?
The diameter across the top of each Bear's porridge bowl was three times the height.

Father Bear's bowl was $24$ cm across. What was the diameter of Mother Bear's bowl and the height of Baby Bear's bowl?
A little girl lived with the three Bears. (Her name was Goldilocks - but you knew that too!)

Goldilocks had all the same things as the bears, but hers were all sorts of odd sizes, some nearly as big as Father Bear's, and some almost as small as Baby Bear's!

Who did all these beds belong to? You might need to do some measuring!
Father Bear's spoon was $30$ cm long. Goldilocks' spoon was five sixths of that.

What proportion of Goldilocks' spoon was Baby Bear's spoon?
Why do this problem?
This problem is based on the story of the three bears which is a good context in which to talk about ratio and proportion. In this case, it leads on to calculating with fractions.
Learners will need to be familiar with finding simple fractions of quantities before tackling this problem.
Possible approach
You could start by telling, or re-telling, the story of the three bears. Many children miss out on traditional English stories and the background is helpful here.
After this you could introduce the problem itself so that the group can discuss it. One of the difficulties of this topic is using the language appropriately, and the more you can encourage the class to talk about the relative sizes of the bears' and Goldilocks's things, the better.
Next learners could work in pairs using this sheet so that they are able to talk through their ideas with a partner. They will be able to check that their solutions seem reasonable, given the information at the start of the problem and should be encouraged to do so.
The discussion at the end should consider the ideas about fractions and proportion introduced in the problem as well as the different answers to the questions posed. This is a good opportunity to check that the group are using the language appropriately and with understanding.
Key questions
If Mother Bear's chair is three quarters of the height of Father Bear's, what is one quarter of the height of Father Bear's chair?
So can you work out how tall Father Bear's chair is?
How can you work out the diameter of Baby Bear's bowl from the diameter of Father Bear's?
Why don't you try measuring the height of the beds?
What does it tell you about the sizes of the three bears at the beginning of the problem?
Possible extension
Learners could try these similar problems - Orange Drink or Timber!.
Possible support
Suggest starting by drawing the bears' chairs on squared paper and counting squares or trying this shorter, and therefore less daunting, problem - Cherry Buns.

