Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Cubes Within Cubes Revisited



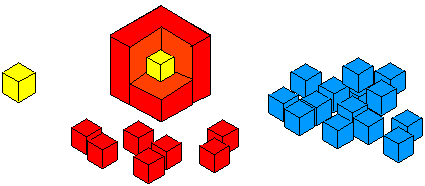
This is then covered with a layer of blue cubes.
How many red cubes have you used?
How many blue cubes have you used?
Find an easy way of working this out.
Now imagine adding a layer of green cubes.
How many green cubes are needed?
Have you a quick method for working out the amounts that you would need for each layer?
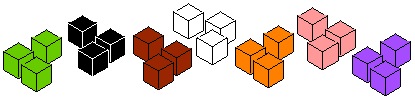
Martha thought about the third layer like this:
- The whole of the new cube is a $5$ by $5$ by $5$ cube.
- The inner layers made a $3$ by $3$ by $3$ cube.
- So the new layer is $5^3 - 3^3 = 125 - 27$ cubes.
Can you see it like this?
Using this method, if you have an $x$ by $x$ by $x$ cube, can you explain how to find an expression for the number of cubes needed to make the next layer?
Emma made the third layer like this:
- First she added a $5$ by $5$ plinth to the bottom, and another to the top.
- Then she added a $3$ by $3$ block to each vertical face, and finally four columns of $3$ cubes to the corners.
Can you see it like this?
Using this method, if you have an $x$ by $x$ by $x$ cube, can you explain how to find an expression for the number of cubes needed to make the next layer?
Charlie made the third layer like this:
- First he added a $3$ by $3$ block to the top and another to the bottom.
- Then he made lots of pillars of $5$ cubes, and wrapped $16$ of these round the sides
Can you see it like this?
Using this method, if you have an $x$ by $x$ by $x$ cube, can you explain how to find an expression for the number of cubes needed to make the next layer?
Can you show that all three expressions are equivalent?
Can you find another way to think about this problem?
Show how you form your expression, and show that it is equivalent to the examples above.

