Pythagorean Triples

How many right-angled triangles are there with sides that are all integers less than 100 units?

Paving the Way

A man paved a square courtyard and then decided that it was too small. He took up the tiles, bought 100 more and used them to pave another square courtyard. How many tiles did he use altogether?

A square patio was tiled with square tiles all the same size. Some of the tiles were removed from the middle of the patio in order to make a square flower bed, but the number of the remaining tiles was still a square number. What were the dimensions of the patio and the flower bed?

Liethagoras' Theorem

Stage: 2 and 3

Article by NRICH team

In another article we looked at Pythagoras' theorem about right-angle triangles. It says that if you square the longest side (called hypotenuse) it will equal the squares of the other two sides added together.

When drawing one of these it doesn't matter what length you make the first side, the theorem will always work. For example, if I made the bottom side 6 cm and the small side 2 cm, I can work out the longest side by...

(6 x 6) + (2 x 2) = (longest side x longest side)

36 + 4 = 40

so 40 = (longest side x longest side)

Now we have to find the square root of 40. A calculator is helpful because the answer is somewhere in between 6.32 cm and 6.33 cm.

So most sets of three side-lengths will have a fraction in them. You have to work quite hard to find lengths for each side that are all whole numbers. These sets of three whole numbers are called Pythagorean Triples, like 3, 4, 5. ($3^{2} + 4^{2} = 5 ^{2}$; that is 9 + 16 = 25) Another Pythagorean Triple is 5, 12, 13 . Another is 7, 24, 25 . What do you notice about these sets of numbers?

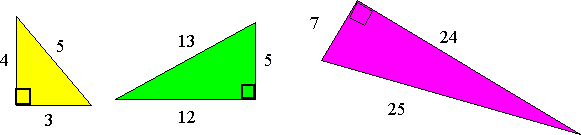
Now here's a bit of fun from Allan White (Australia):

Liethagoras (say "Lie-thag-or-us" - get it?!) was a long distant cousin of Pythagoras. He was very jealous of Pythagoras, because his theorem had given number triples that gave right triangles such as 3, 4, 5 or 5, 12, 13 or 7, 24, 25. So he thought, "If only I could come up with a theorem that was simpler than Pythagoras, then I too would be famous". So he thought and he thought until he had a wonderful thought and he rushed off to tell the mathematicians.

His theorem was: In any right triangle the square of the smallest side equals the sum of the other sides.

For example:

In the 3, 4, 5 Triangle 3 x 3 = 4 + 5

In the 5, 12, 13 triangle 5 x 5 = 12 + 13

Does it work for the 7, 24, 25 triangle?

Instead of becoming famous, the mathematicians just laughed at him. Why did they laugh at him?

Let's investigate:
1. Can you find a number triple that obeys Liethagoras' theorem but doesn't obey Pythagoras' theorem and so doesn't give a right triangle?

2. Can you find a number triple that obeys Pythagoras' theorem but doesn't obey Liethagoras' theorem?

3. Liethagoras' theorem only works on Pythagorean triples that ...

That's something for you to work on.

Visualising. Pythagorean triples. Angle properties of shapes. Mixed triangles. smartphone. Area. Circles. Squares. Pythagoras' theorem. Mathematical reasoning & proof. Quadrilaterals.

You may also like

Pythagorean Triples

Paving the Way

Patio

Liethagoras' Theorem

Stage: 2 and 3