Last Biscuit
Can you find a strategy that ensures you get to take the last biscuit in this game?
This game follows on nicely from Have You Got It?
Last Biscuit printable worksheet
This is a game for two players. You can play against the computer or with a friend.
It is a version of a well known game called Nim.
Each player can take biscuits in one of two ways:
- By taking any number they like from just one jar or
- By taking the same amount from both jars.
The winner is the person who takes the last biscuit/s.
Play the game several times.
Can you find a winning strategy?
Can you always win?
Does your strategy depend on whether or not you go first?
Can you work out a winning strategy for any combination of biscuits?
Look for patterns in your winning moves and use them to find winning strategies.
Can you describe the winning strategy if the jars start by containing 100 and 50 biscuits?
Start by playing Have You Got It?
Can you find a winning strategy?
Work backwards.
Simplify the game by choosing a smaller number of biscuits in each jar and working out a winning strategy.
Play the game against the computer and think about the computer's strategy.
Well done to everyone who sent in a solution. Some people noticed that it is possible to take 0 biscuits from each bag and used this to win. However, this is not really a strategy to win the game, just to trick the computer.
Imogen from Wycombe High School in England suggested:
Change the settings to 4 on each side and take them
Ivan from Aquinas Catholic School in Australia, Bouis from Abingdon in the UK, H from PMS and Zoha from Wycombe High School described a strategy that works if you go first with 4 and 8. This is H's work:
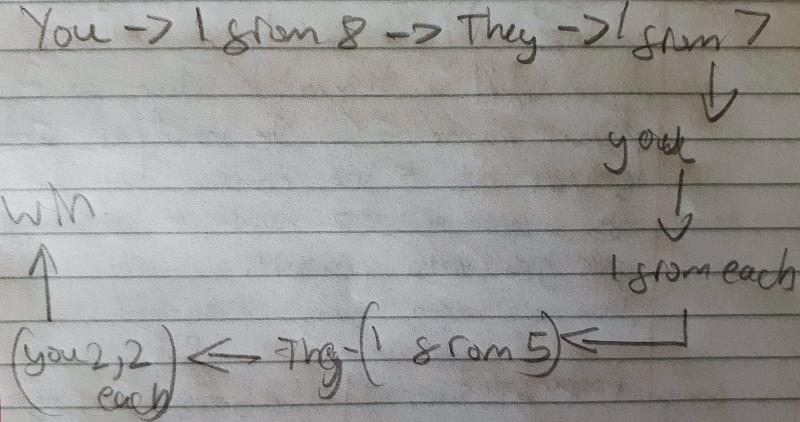
Nayanika from the Tiffin Girls' School in the UK, Anya from Tanglin Trust School in Singapore, Charlie from Heckmondwike Grammar School in the UK described a strategy for the final moves of the game. This is Charlie's work:
I think the strategy is that you need to try and get the biscuits with two in one jar and 1 in the other and it is your opponent's go. Because when you get to that point the opposition can either:
Take one from the glass with two in it but then you can just take on from each side and win
Take one from the glass with one in it but then you can just take two from the other glass
Take one from both sides but then you can just take away 1 from the glass with 1 left
Take two from the glass with two in it but then you can just take one from the other glass
Avipsa from India, Anya, Nayanika and Abhigyan described some ways of getting to this winning position of (2,1). This is Anya's work:
From the above conclusion, we can get some winning strategies:
a) If there are $n$ biscuits in one jar and $n+1$ in the second, you can take $n-1$ biscuits from each jar to make the new amount of biscuits (1,2). Using what we found out previously, no matter what the other person plays after
this, you can take all biscuits in your next turn and win.
b) If one of the original jars starts with 1 biscuit, you can take the required amount of biscuits from the other jar to make the other jar have 2 biscuits. Now the new configuration is (1,2) and therefore you win.
c) Similarly, if one of the original jars starts with 2 biscuits, you can take the required amount of biscuits from the other jar to make the other jar have 1 biscuit. Now the new configuration is (1,2) and therefore you win.
Shuvom, Grihith and Trayee from the Future Foundation School in India and Anya found another winning position. Shuvom wrote:
We should make a situation where its 3 biscuits in 1 jar and 5 biscuits in the other jar and its the opponents turn.
YingGe from Headstart in China explained why:
As long as the person gets 5:3, (or a 1 or 2 appears in one of the jars), the opponent will lose. Because in the 5:3 case, the person who is going to take next will never make 1:2 by [themself]. Only these values are available
{4:3,2:3,3:3,1:3, 5:2,5:1, 4:2,3:1}.
From each combination, you can either win directly or leave your opponent with (2,1)
YingGe also showed that (7,4) is a winning position:
The strategy is if you take 1 from the jar with 8 biscuits(7:4), the other people will lose at the same time.
Case 1: The 2nd person takes 1 from the jar with 4 biscuits(7:3),you can take 2 from the jar with 7 biscuits (5:3). Once you get 5:3, the 2nd person will lose.
Case 2: The 2nd person takes 2 from the jar with 4 biscuits(7:2), the 1st person can take 6 directly from the jar with 7 biscuits to make 1:2.
Case 3: The 2nd person takes 3 from the jar with 4 biscuits(7:1), the 1st person can take 5 directly from the jar with 7 biscuits to make (2:1)
(do not take 4 from the jar with 4 biscuits=stupid to do that)
Case 4:The 2nd person takes 1 from both jars(6:3), the 1 st person can take 1 from the jar with 6 biscuits left(5:3). Then the 2nd person can take any, but he will still lose (the same as the explanation above the question.)
Case 5: The 2nd person takes 2 in both jars(5:2). As long as the number 2 appears, the person will definitely lose.
Case 6:The 2nd person takes 3 in both jars(4:1). As long as the number 1 appears the person will definitely lose.
Case 7:The 2nd person takes 1 in the jar with 7 biscuits left(6:4), then the 1st person can take 1 in both jars to make it 5:3. The cases next are the same as the above.
Case 8: The 2nd person takes 2 in the jar with 7 biscuits(5:4), then the 1 st person can take 1 in the jar with 4 biscuits to make (5:3).The cases next are the same as the above.
Case 9: The 2nd person takes 3 in the jar with 7 biscuits(4:4)=lose definitely
Case 10: The 2nd person takes 4 in the jar with 7 biscuits(3:4), then the 1 st person can take 2 in both jar to make (1:2)=First person will win.
Case 11: The 2nd person takes 5 in the jar with 7 biscuits(2:4), then the 1 st person can take 3 in the jar with 4 biscuits to make (2:1).
Case 12: The 2nd person takes 6 in the jar with 7 biscuits(1:4), then the 1 st person can take 2 in the jar with 4 biscuits to make (1:2).
Case 13: The 2nd person takes 7 in the jar with 7 biscuits(0:4)=lose definitely.
YingGe then made a prediction:
1st Prediction : If 2 jars have an even number of biscuits, the person who goes first will win. If 2 jars have an odd number of biscuits, the person who goes second will win. If one jar has the odd number of biscuits and one jar has an even number of biscuits, the person who goes first will win.
Test:
[YingGe found that this works if the difference between the numbers of biscuits is 1 or 2, but that starting from (1,5), (3,7), (5, 9) or (7,11) the first player wins.]
The first prediction is wrong.
This is Nayanika's strategy to land on winning positions:
If the jar with the lesser number of biscuits has $n$ biscuits, generally, the pattern is:
When the difference between the two jars is 2, and $n\gt$3, take 3 from each jar away.
When the difference between the two jars is 3, and $n\gt$5, take 5 from each jar away.
When the difference between the two jars is 4, and $n\gt$7, take 7 from each jar away.
YingGe made another prediction:
2nd Prediction:
The chance for the 2nd person to win is very rare. The 2nd person wins only when the number of biscuits is at its specific numbers. For example:
Possible numbers
1:2
1(+2) :2 (+3) =3:5
3(+1);5(+2)=4:7
6(+2):10(+3)=8:13
8(+1);13(+2)=9:15
9(+2):15(+3)=11:18
11(+1):18(+2)=12:20
12(+2):20(+3)=14:23
In that case, the final winning strategy is get these number ratio above to make the person who goes next loss.
Anya found these same winning positions and noticed some patterns:
If you look at these pairs of numbers, you can see that there is a pattern in them. Each time, the difference between the numbers of biscuits in each jar increases by 1.
For example:
2 - 1 = 1
5 - 3 = 2
7 - 4 = 3 etc.
Mahdi from Mahatma Gandhi International School in India used a diagram to show how you can always win the game. Mahdi began by comparing this game to NIM. Click to see Mahdi's explanation of the game NIM.
This strategy involved thinking backwards. If the opponent is left anywhere from 1 to 9, then they can win. But at 10, they are certain to loose. So, I had to force the total to be at 10 when it’s their turn. Now, my target to reach shifted from going to 10 instead of 0 at the moment. Again, If I want to force the opponent to leave them at 10, I can make that happen if I make them reach till 20. Continuing on, I would have to leave them at 90. Moving on last step, the total should be 100 and It should be the opponents turn for me to win.
For example, if they begin by saying 96 after subtracting 4, I can make the total go to 90 by subtracting 6. From 90, they subtract 7 and I subtract 3. It’s 80 and their turn now. Chipping away multiples of 10 left the opponent at 10. Now, no matter what number from 1 to 9 they choose, I will definitely have to choose the supplementary of 10 to subtract from. If they subtract 3, I must subtract 7 on the next move to win!
Fun fact, if you rotate the word NIM by 180˚, you get WIN.
Here is Mahdi's excellent work on Last Biscuit. Note that above, we have used 'winning position' to mean 'if it looks like this after your turn, you will win', but Mahdi says 'winning move' or 'winning position' to mean 'if it looks like this at the start of your turn, you will win'.
Why do this problem?
Strategy games are always good for developing mathematical thinking. This game is interesting because although the 'overall' strategy is difficult, students can usefully analyse particular cases. This will require clear recording of results and careful analysis of the logical possibilities.
Possible approach
This problem featured in an NRICH Secondary webinar in June 2021.
You might want to introduce this problem as a follow-up to Have You Got It?
It might become apparent that certain configurations are known to be winning positions (e.g. 2 and 1).
When one of these configurations is found it could be shared with the group. Using known winning configurations might help students find winning configurations for larger numbers of biscuits.
Throughout, clarity of thinking, analysis of the game position and clear recording of results should be encouraged.
Once several winning positions have been found, can any patterns be identified?
Can they use these to find more winning positions?
Key questions
- What is the smallest 'certain lose' position?
- How could we prevent our opponent from putting us into this position?
Possible extension
- Can students prove that (1, 2) is the only winning configuration with a difference of 1 in the total number of biscuits?
- How many winning configurations differ by 2, 3 or n biscuits?
Students might also like to play Nim, which is a version of this game with many more 'jars'.
Possible support
Start by introducing students to Have You Got It? and don't move on until you are satisfied that students can explain clearly why their strategy works.
Can they devise a strategy to win for these individual cases?
