Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Cuboids
Age 11 to 14
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
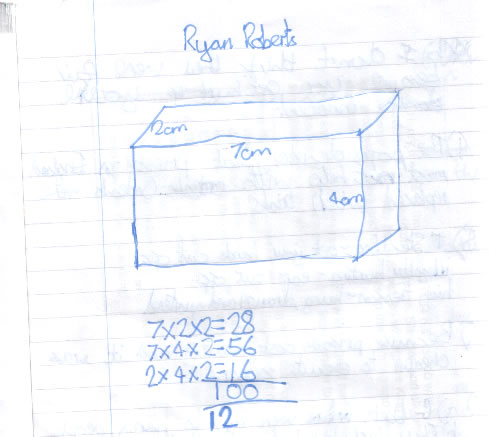
Steven and Ryan found that a 2x4x7
cuboid has a surface area of 100 square units.
Justin from Mason Middle School found that a 1x2x16 cuboid also satisfies the conditions:
I back it up by saying that$1\times 2 = 2$,
$2 \times16 = 32$
and $16 \times1 = 16$
and add them all up and you get $50$, and then multiply by $2$ and you get a square area of $100$!
Megan was able to show that these were the only two possible solutions:
Call the lengths of the 3 dimensions (height, depth, width) $x$, $y$ and $z$.The surface area is $2xy+2xz+2yz$, as the area of each face is calculated by multiplying its two sides together, and there are $2$ of each face.
Hence, $2xy+2xz+2yz = 100$.
Dividing by $2$, $xy+yz+xz = 50$.
I will assume that $x$ is the shortest side and $z$ the longest to avoid repeating solutions. Therefore I must find integer solutions to the equation $xy+yz+xz = 50$ where $x < y < z$.
Rearranging the equation,
$yz+xz = 50-xy$
$z(x+y) = 50-xy$
$z = (50-xy)/(x+y)$.
I used an excel spreadsheet with 3 columns, 1 for each of $x$, $y$ and $z$.
In the $z$ column I write the rearranged formula.
I then started from $x = 1$, $y = 1,2,3...$ looking for integer values of $z$ until I reached a solution which had been repeated (as here $y$ is bigger than $z$, so I would be repeating values with $y$ and $z$ swapped around) or where $z$ became smaller than $y$.
For $x = 1$ I found only 1 solution, $(1, 2, 16)$.
Checking with the original formula this does agree to a total of $100$.
I then continued repeating the procedure with $x = 2$, $y = 2$,$3$,$4$... and found a solution of $(2, 4, 7)$.
With $x = 3$, $y = 3$,$4$,$5$... there are no solutions, as $z$ becomes smaller than $y$ where $y=5$ (and $z = 4.375$) and there are no integer solutions before this.
With $x = 4$, $y = 4,5,6...$ $z$ becomes smaller than $y$ when $y = 5$ $(z = 3.333)$ therefore there are no solutions where $x = 4$.
After $x = 4$, the intitial value of $z$ is always smaller than $y$, therefore there are no further solutions.
The only 2 solutions to the problem are: $(1, 2, 16)$ and $(2, 4, 7)$.
Fred from Albion Heights School also offered some non-integer solutions:
$h = 1$, $w = 1$, $l = 24.5$$h = 2$, $w = 2$, $l = 11.5 $
$h = 4$, $w = 4$, $l = 4.25$
$h = 2.5$, $w = 5$, $ l = 5$
$h = 1$, $w = 4$, $l = 9.2$
Well done to you all.