Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Up and Down Staircases
Age 7 to 11
Challenge Level 





One block is needed to make an up-and-down staircase, with one step up and one step down.

Four blocks make an up-and-down staircase with two steps up and two steps down.
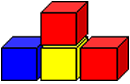
How many blocks would be needed to build an up-and-down staircase with three steps up and three steps down?
What about for four steps up and four steps down?
What do you notice about the number of blocks needed each time?
Can you predict how many blocks will be needed to build an up-and-down staircase with five steps up and five steps down?
Were you right?
Explain how you would work out the number of blocks needed to build a staircase with any number of steps.

