Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Flipping Twisty Matrices



- Problem
- Student Solutions
- Teachers' Resources
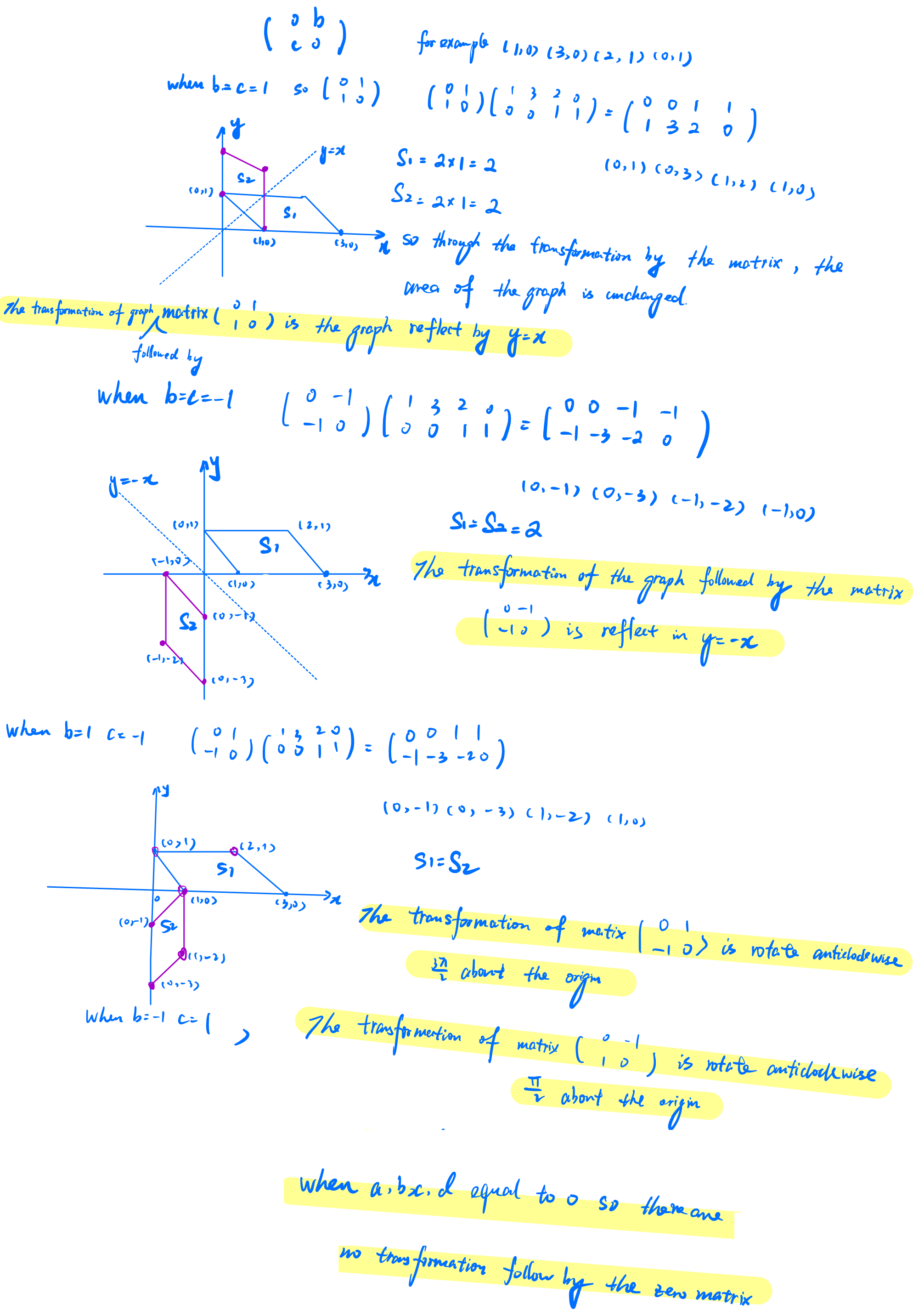
Yiran from Guanghua Qidi in China chose a shape and looked at its image under matrices of the form $ \left( \begin{array}{cc} 0 & b \\ c & 0 \end{array} \right) $ where $b$ and $c$ can take the values $1$ and $-1.$ This is Yiran's work (click on the image to open a larger version). Note that for $b=1, c=-1$ the rotation is actually clockwise,
not anticlockwise - as shown in Yiran's diagram.
Andrei from School No. 205, Bucharest, Romania considered matrices of the form $ \left( \begin{array}{cc} a & 0 \\ 0 & d \end{array} \right) $ where $a$ and $d$ can take the values $1$ and $-1.$ Andrei also looked at more general points under both families of matrices. This is Andrei's work:
1. $b = c = 0,\ a = d = -1$ $$ \left( \begin{array}{cc} -1 & 0 \\ 0 & -1 \end{array} \right) \left( \begin{array}{c} x \\ y \end{array} \right) = \left( \begin{array}{c} -x \\ -y \end{array} \right) .$$ This means each point (x, y) transforms into its symmetrical image with respect to the origin, i.e. into the point (-x, -y). This is a rotation of
180 degrees about the origin.
2. $b = c = 0,\ a = - 1,\ d = 1$ $$ \left( \begin{array}{cc} -1 & 0 \\ 0 & 1 \end{array} \right) \left( \begin{array}{c} x \\ y \end{array} \right) = \left( \begin{array}{c} -x \\ y \end{array} \right) .$$ Here, it is a reflection in the y-axis.
3. $b = c = 0,\ a = d = 1$ $$ \left( \begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array} \right) \left( \begin{array}{c} x \\ y \end{array} \right) = \left( \begin{array}{c} x \\ y \end{array} \right) .$$ In this situation each point transforms into itself.
4. $b = c = 0,\ a = 1,\ d = -1$ $$ \left( \begin{array}{cc} 1 & 0 \\ 0 & -1 \end{array} \right) \left( \begin{array}{c} x \\ y \end{array} \right) = \left( \begin{array}{c} x \\ -y \end{array} \right) .$$ This transformation leaves the abscissa unchanged and modifies the sign of the ordinate, being a reflection in the x-axis.
Now, I look at the next set of transformations.
5. $a = d = 0,\ b = c = 1$ $$ \left( \begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array} \right) \left( \begin{array}{c} x \\ y \end{array} \right) = \left( \begin{array}{c} y \\ x \end{array} \right) .$$ In this transformation, the abscissa and the ordinate are interchanged, the transformation being a reflection in respect to the line $y=x$, the angle
bisector of the first quadrant.
6. $a = d = 0,\ b = 1,\ c = -1$ $$ \left( \begin{array}{cc} 0 & 1 \\ -1 & 0 \end{array} \right) \left( \begin{array}{c} x \\ y \end{array} \right) = \left( \begin{array}{c} y \\ -x \end{array} \right) .$$
Andrei also concluded that this is a rotation of $90^\circ$ clockwise about the origin.
7. $a = d = 0,\ b = c = -1$ $$ \left( \begin{array}{cc} 0 & -1 \\ -1 & 0 \end{array} \right) \left( \begin{array}{c} x \\ y \end{array} \right) = \left( \begin{array}{c} -y \\ -x \end{array} \right) .$$ This corresponds to a reflection in the line $y=-x$.
8. $a = d = 0,\ b = -1,\ c = 1$ $$ \left( \begin{array}{cc} 0 & -1 \\ 1 & 0 \end{array} \right) \left( \begin{array}{c} x \\ y \end{array} \right) = \left( \begin{array}{c} -y \\ x \end{array} \right) .$$ This corresponds to a rotation of the point by 90 degrees anti-clockwise about the origin.