Magic triangle
Problem
Place the digits 1 to 9 into the circles so that each side of the triangle adds to the same total.
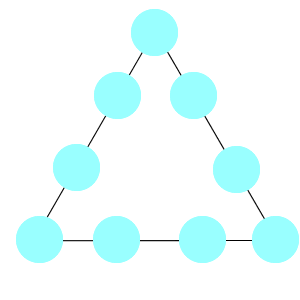
Can you find more than one solution?
Student Solutions
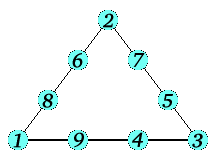
Michael and Robert from Necton Middle School in Norfolk sent the following solution, where the sides all add up to 17:
Simone from Stroud Green Primary School sent us another solution where the sides all add up to 17.
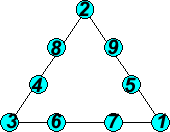
In fact, there are lots more solutions. Here's a list of them (including the two shown above). Each group of four numbers makes up a side of the triangle. Of course, within a side you can switch round numbers that aren't on a corner, but that doesn't really give any new solutions.
Teachers' Resources
Why do this problem?
This is a 'low threshold high ceiling' problem in that all children will be able to find at least one solution through trial and improvement, but others will use logical thinking to develop and try out different strategies for making the sides equivalent.
Possible approach
There are different layers to this activity, making it ideal for a whole class task.
When someone gets all three sides the same, stop the class and record the result on the board. Ask if they think this is the only way we could place the numbers to make the sides equivalent. Allow some time for exploration and if possible make a part of the wall space available for recording all the children's answers. If you encourage the children to record each solution on a separate piece of paper you can rearrange them during discussion.
You might choose to leave this as a 'simmering' activity over a period of a few days. Not all children will engage with it but some will become very enthusiastic. In the plenary discussion draw attention to families of solutions, and the upper and lower limits for the side totals.
Key questions
Possible extension
Providing a public space for the children to record their own investigations makes it a more collaborative activity.
Possible support
Children who find this difficult could begin with an easier activity using six circles, three on each side, and the numbers 1-6. Begin by giving them 15 buttons or counters to place in the circles so that there are the same number of counters on each side. This gives visual support. Move from there into having a different number of counters in each circle, and from there to using digits rather than counters.
