Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
1, 2, 3, 4, 5
Age 7 to 11
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
1, 2, 3, 4, 5
Using the numbers $1, 2, 3, 4$ and $5$ once and only once, and the operations $\times$ and $ \div$ once and only once, what is the smallest whole number you can make?
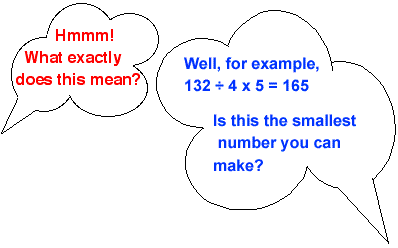
Why do this problem?
This short problem could be used to start a lesson or fill a gap made by those who finish early. It will promote thinking about numbers and offers opportunities to practise multiplication and division.Key questions
What results can you find obeying these rules?
Why don't you put all your answers in order?
What things do you notice about your different results?
Why do you not get any divisions by $5$?
Does it help to multiply by $1$? If not, why not?

