Smaller and Smaller
Problem
Here is an equilateral triangle which has sides of length 1 unit:
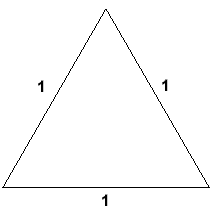
We could take out the middle third of each side and replace it with a spike. If the spike is made of two lines which are the same length as the missing section, it will look like this:
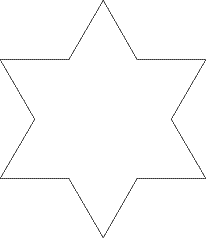
We could do the same again. Taking out the middle third of each line and replacing it with a spike in the same way gives this:
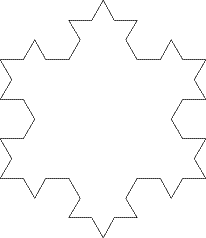
Remembering that the length of each side of our original equilateral triangle is 1 unit, what is the perimeter of the first shape we drew above? And the second? Can you see a pattern? Perhaps you can explain why this pattern comes about.
Can you predict, without drawing, what the perimeter of the next shape will be if we continue drawing them in the same way?
Could you predict the perimeter of any shape in the series?
The shapes above are called fractals. A fractal is made up of lots of copies of itself, each one smaller than the last. See also the problems Von Koch Curve, The Cantor Set and How Long is The Cantor Set?
Getting Started
Try leaving the lengths as top-heavy fractions.
Student Solutions
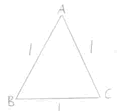
Caroline and Bronya from Tattingstone School sent wonderfully explained solutions to this problem. Caroline drew some diagrams to help her:
|
Image
|
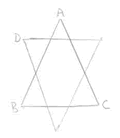
Side AB = 1 Perimeter = 3 x 1 = 3 |
|
Image
|
Side ADB = 4 x 1/3 =
4/3 Perimeter = 3 x 4/3 = 4 |
|
Image
|
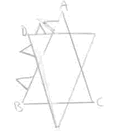
Side ADB = 4 x 4/9 =
16/9 Perimeter = 3 x 16/9 = 48/9 = 16/3 = 5 1/3 |
She explains:
The pattern is every time you add on a new smaller spike you multiply by 4 and divide by 3.
Here, Bronya describes how she approached the problem:
First of all I looked at the perimeter of the equilateral triangle. It was 3 units. Then I looked at the perimeter of the star. If one side is 11/3 units then the perimeter is 4 units. Then the perimeter of the third shape. I looked at a section like this:

Each section = 1/3 + 1/9 unit = 3/9 + 1/9 = 4/9 unit
There are 12 sections so the total perimeter = 4/9 x 12/1 = 48/9
I looked at all the perimeters as ninths:
Perimeter 1 was 27/9
Perimeter 2 was 36/9
Perimeter 3 was 48/9
Each time the perimeter increases by one third.
I think this comes about because in each section a third of the section is added on.The perimeter of the next shape would be 64/9 because:
48 divided by 3 is 16 therefore increase 48/9 by 16/9
Total would be: 48/9 + 16/9 = 64/9
Thank you to you both - these are very well reasoned solutions. I wonder whether you could generalise to any shape in this series?
