Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
LOGO Challenge 9 - Overlapping Polygons
Age 7 to 16
Challenge Level 





- Problem
- Teachers' Resources
LOGO Challenge 9 - Overlapping Polygons
TO POLY :N
REPEAT :N [ FD 40 RT 360/:N]
END
It was while experimenting with the procedure above that the three overlapping motifs below were produced. In each case the motif is a regular dodecagon.
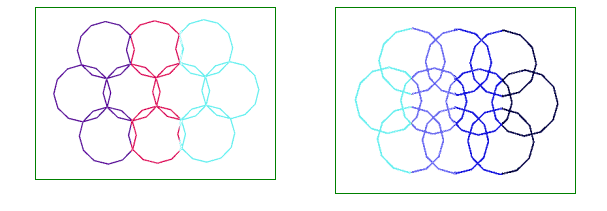
 |
Why not experiment with different values of N?
To what extent will sets of Ngons overlap and produce differing tiling patterns? |
What happens if N is very large? You might want to make the distance you travel forward smaller to see what happens. If you are struggling, why not look at First Forward into LOGO numbers 4 and 6 and also in LOGO Challenge 10 - Circles .
Try some substitution for different values of N and see how this helps you to draw different polygons.
Try N = 3. Why isn't the answer 60, which is the size of the angle of an equilateral triangle?
N.B. As you walk around any polygon what is the total angle you will always turn through no matter what the size of the polygon?
360 degrees - which is the sum of the external, not the interal angles.

