Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Published 2003 Revised 2012
Conic Sections

During a dark night in a dark room, shine a bright torch light with a rounded head on to the floor. Point the torch straight down; you should get a disc shape. Turn it slightly and the disc becomes distorted. If you rotate the torch far enough, the image on the floor will stretch away from you indefinitely (provided your room does likewise). The outlines of the shapes formed by the torch on the floor are known as the conic sections: the distorted disc is called an ellipse until it stretches off to infinity when it becomes a hyperbola. At the precise torch angle for which the ellipse becomes a hyperbola, the special curve produced is known as a parabola. In this article we investigate some of the fascinating geometry of conic sections with as little algebra as possible. All the details may be appreciated by anyone with only a basic knowledge of algebra and geometry although the relevant diagrams themselves require some attention.
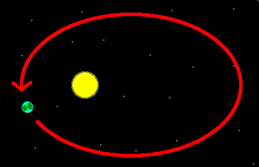
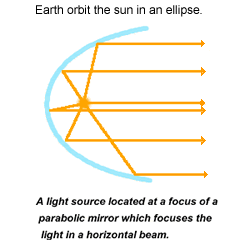
Since their first discovery, credited to a Greek man Menaechmus from around 350 BCE, conic sections have been observed in a variety of situations. The Earth travels round the sun in the shape of an ellipse, radio dishes and car headlights are parabola shaped because of the way light is reflected from their surface (radio dishes receiving light and car headlights emitting light) and in my own research I recently came across these curves while investigating convergence criteria of continued fractions.
We now have a fair few examples of.... what exactly? The Greeks gave the official definition of conic sections as the curves formed through the intersection ('section') of a cone ('conic') and a plane. The curves are the outlines of the intersecting region. In the example at the beginning, the cone was the beam of the torch, the plane was the floor and the intersection was the image on the floor. It has since proved most consistent to define the conic sections as the curves formed through intersecting a plane and two cones, one above the other. The next set of diagrams illustrate this. Each pair of cones has been sliced through by a plane shown in pink.
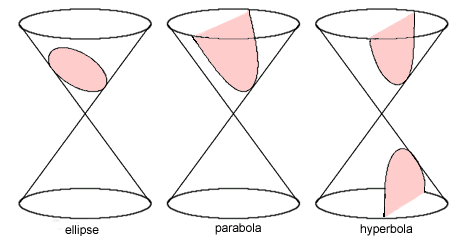
Notice how in each diagram we have kept the cones fixed and rotated the plane round. When the plane is horizontal, the intersection is a special case of an ellipse, a circle. If the plane is turned so that it lies at the same angle as the slope of the cone then the intersection is a parabola. Rotate the plane still further and the intersecting curve is a hyperbola. There are various special cases that can arise, which we are not especially interested in as they are not especially interesting. For instance, if the plane is horizontal and passes through the vertices of the cones then the intersection is a point (can you think of the other special cases?)
The ingeninuity in this Greek definition is that we have described two dimensional curves in a three dimensional manner. If disaster befell the universe and we somehow lost a dimension (unlikely- don't have nightmares) then with only this definition we would lose the conic sections! With this threat in mind we now develop purely two dimensional definitions of the curves. They are shown in below in green. The additional geometry is explained after the diagrams.
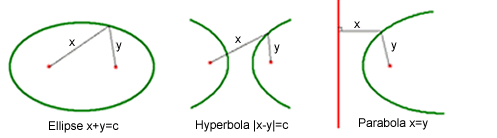
In all three diagrams there are fixed red points called foci (singular: focus ). The red line is also fixed and is called the directrix . An ellipse can be constructed by taking two fixed foci and a given positive constant c; it then consists of those points (shown in green) that lie at distances x and y from the two foci, where x+y=c. You can draw an ellipse on paper by hammering two nails through the paper into your desk (which are the foci) and attaching a length of string (shown in grey in the diagram) at each end to the nails. Now stretch the string as far as possible with a pencil and trace the curve formed under this full extension. There is an advantage in using a loop of string encircling the two nails with a pencil inside, rather than a length of string. Why might this be better?
The hyperbola is similar. Again we have two fixed foci and a fixed positive constant c. The green locus then consists of those points that lie at distances x and y from the foci where either x-y=c (giving one half of the hyperbola) or y-x=c (giving the other half).
The parabola differs in that we have only one fixed focus, but also a fixed line (the directrix). The parabola consists of those points that are the same distance from the focus and the directrix. In more detail, take a green point in the locus of the parabola and draw a line from this point to the directrix, perpendicular to the directrix. Let the length of this line be x, then the distance from the green point to the focus must also be x. The diagram shows the mathematics much more clearly than this explanation.
The key question now is how these plain plane conic section developments are reconciled with the original Greek version. The following justification of their equivalence is based on ideas first conceived by Germinal Dandelin in 1822 and are some of my favourite bits of mathematics.
The Ellipse
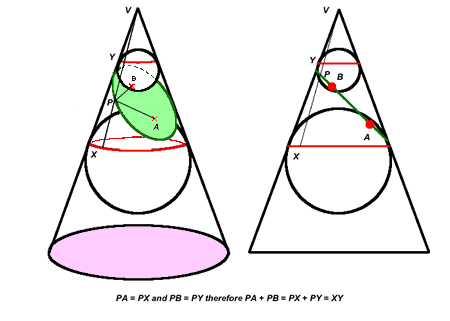
The idea behind the above complicated looking diagrams is absolutely amazing and it is well worth putting in the effort to work out what is going on. The left hand picture is a depiction of the cone in three dimensions and the right hand picture is a side view. Imagine a plane cutting through the cone (shown in green). Two spheres are wedged into the cone so that they touch the plane at points A and B (one above and one below) and they must also touch the cone at every point around a circle (shown in red). Consider any point P on the green intersecting curve and join it to the vertex by a straight line along the side of the cone (cutting the red circles at X and Y). The lines through PX and through PA are both tangent to the bigger sphere and hence the distances between PA and PX are equal. Similar reasoning applies to give PB=PY and therefore PA+PB=XY, which is a constant- just the fixed distance between the two red circles. Persevere with this!
The Hyperbola

The geometry here is similar. This time the plane intersects both cones, again shown in green. The spheres must be placed one in each cone and they intersect the plane at points A and B and intersect the cone in circles, again shown in red. We take any point P on the hyperbola (dark green) and draw a straight line from it through the vertex of the cone, passing through the red circles at points X and Y. The distances PA and PX are equal since both A and X lie on the sphere. Similarly PB=PY. Hence PB-PA=PY-PX and the latter expression equals the constant distance c between X and Y. Set PB=x and PA=y and we recover the equation of one branch of the hyperbola, x-y=c. The other branch has equation y-x=c.
The Parabola
This time a plane cuts through the cone at the same angle as the cone and only one sphere fits in above this plane corresponding meeting the cone at the one focus and in a red circle. This red circle lies in a plane which meets the green plane in a line which is the directrix. Try drawing diagrams similar to those shown for the ellipse and hyperbola to obtain the two dimensional definition of a parabola from the three dimensional Greek definition.
Now well established in two dimensions, we conclude this article by obtaining a succinct definition of conic sections which is valid in a flat 2D world.
Recall that our ellipse has equation x+y=c and draw a circle of radius c about one of the foci, marked A:
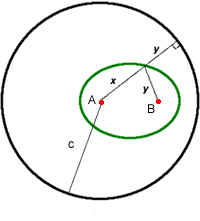
Imagine the length of string which is tied at each end to the foci. Undo the end that is not in the centre of the circle and stretch it out to its maximum length. It will extend a distance x+y=c and reach the circle; we could draw the circle like this. The diagram shows the string both attached and detatched from the second foci B. The (shortest) distance from a point on the ellipse to the circle is equal to the radius of the circle minus the distance from the ellipse B, that is c-x = y. Thus the ellipse consists of those points that are the same distance ('equidistant') from the other focus A and the circle. Try this yourself: draw a circle and mark a point somewhere inside it. Now plot those points which are equidistant from this fixed point and the circle, remembering that the distance from a point to a circle means the shortest distance between them which is along one of the radii.
The geometry alters if the circle of radius c drawn about one of the foci does not contain the other focus.
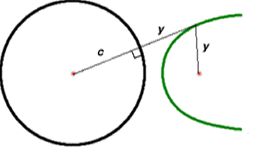
If a green point outside the circle lies at the same distance y from the outside focus and from the circle then it must lie at a distance x=y+c from the circle centre. Hence x-y=c and one branch of a hyperbola is recovered.
Thus we may define (one branch of a hyperbola) as consisting of those points that lie at the same distance ('equidistant') from a fixed circle and a fixed point. If we combine these ellipse and hyperbola observations together with our two dimensional parabola description then we arrive at the following definition (as usual, there are special cases to explore, plus this definition suffers from ignoring a branch of the hyperbola):
A conic section is the loci of points equidistant from a fixed line/circle and a fixed point in the plane.
Investigations:
(1) EASY! Our ellipse has equation x+y=c. Fixing c, what happens as the two foci approach each other, how do the corresponding ellipses change accordingly? What happens if the foci meet up? What if they vastly separate? Experiment similarly for the hyperbola. See if you can interpret our two dimensional description of the parabola as a 'limiting case' of the hyperbola by greatly separating the foci then concentrating on the branch of the hyperbola near one particular focus.
(2) MEDIUM! Establish the light focusing property of parabolas. Specifically, if a beam of light leaves the focus of a parabolic mirror then it will reflect off the surface of the mirror in a direction perpendicular to the directrix of the parabola
(3) HARD! There is another definition of the conic sections in two dimensions which is often how students are first introduced to the topic. Consider a fixed line and a fixed point and consider the locus of points at a distance s from the line and a distance t from the point. We have already seen that the parabola has equation s=t. If we now introduce a positive number e and consider the equation t=es then for 0< e < 1 an ellipse is obatined and for e > 1 a hyperbola is obtained. It is possible to establish these relations from the three dimensional definition in a similar manner to how we obtained the s=t case for the parabola. Have a go!

