Volume of a pyramid and a cone
These formulae are often quoted, but rarely proved. In this article, we derive the formulae for the volumes of a square-based pyramid and a cone, using relatively simple mathematical concepts.
(The ideas used in this article are also used here to find the volume of a sphere and the, impressively named, mouhefanggai shape.)
What you need to know.
You need to be familiar with the formulae for the area of a square, the area of a circle, and the volume of a cuboid. We will also use ideas of enlargement and ratio.
The yangma.
When we think of a pyramid, we usually think of one where the vertex (the top point) is above the centre of the base, a right pyramid . However in this article, we will begin with a yangma. Yangma is an ancient Chinese name for a rectangular-based pyramid whose vertex is vertically above one of the vertices of the base. We will take a yangma with a square base of side length $a$, and height also length $a$. Three of these can be fitted together to form a cube.

Since we know that the volume of the cube is $a \times a \times a = a^3$, it follows that the volume of each of these yangmas is $\frac{a^3}{3}$.
Enlargement
Consider, for a moment, a cube with edges 1 unit long. You know that the volume is $1 \times 1 \times 1$. Now stretch that cube in a horizontal direction so that it measures a by 1 by 1. Its volume is now $a \times 1 \times 1$. If we imagine the cube sliced horizontally, there will be the same number of slices, but each will be a times as long.

If we stretch the cube in a perpendicular direction, so that it measures a by b by 1, the volume will be $a \times b \times 1$, or $b$ times larger. If we stretch the cube in the third perpendicular direction, by a scale factor of $c$, the volume will be $a \times b \times c$, which we know as the formula for the volume of a cuboid.
There are three independent directions in which we could enlarge a 3D shape. If we enlarge it by a scale factor $k$ in one of these directions, the volume will be $k$ times as large.
Back to our yangma:

Suppose we want the volume of a yangma whose height is different to the base lengths, perhaps height $h$ instead of a. Well, this is just an enlargement in the vertical direction.
The scale factor? If we are turning $a$ into $h$, we have multiplied by $\frac{h}{a}$.
So the volume of our new yangma is $\frac{h}{a} \times \frac{a^3}{3}$, or $\frac{a^2h}{3}$.
Sliding the slices
We now have a formula for the volume of any square-based pyramid whose vertex is above one of the vertices of the base. What about if the vertex is somewhere else - the middle, for instance? What we are going to do is to imagine the pyramid cut into lots of slices horizontally. We are going to slide these slices across, so that the top of the pyramid is above the middle of the base.
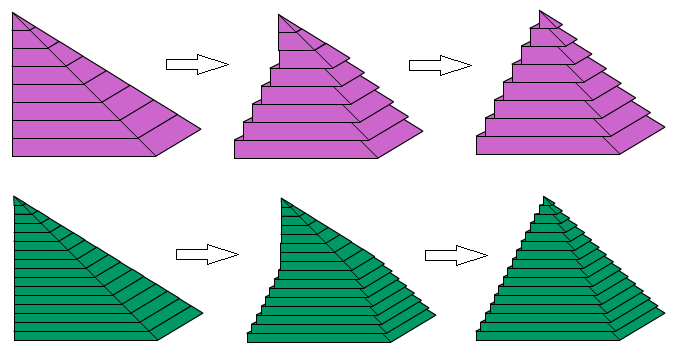
If we had an infinite number of slices, our pyramid would have nice straight edges. You can probably imagine that with more slices, it would look smoother than in this illustration. Has the area of any of the slices changed? So has the volume of the shape changed?
We can now see that the volume of any square-based pyramid is $\frac{a^2h}{3}$.Comparing a cone with a pyramid
We will now look at a cone. We'll start with a right cone , whose vertex is above the centre of the base. In fact, by slicing it as in the previous section, we can show that the same formula applies for any cone.
Imagine a cone whose base is a circle radius $r$, and height is $h$. This cone will fit exactly inside a square-based pyramid with base length $2r$ and height $h$.Image

|
Image
|
Suppose we take a slice of the pyramid with the cone inside, from some way up the pyramid. This will look like a square with a circle fitting inside. We don't know the radius of the cone at this point, so we'll call it $x$.
The area of the square is $2x \times 2x=4x^2$.
The ratio of the circle to the square is $\pi : 4$.

The same is true for every slice we take: the area of the circle is $\frac{\pi}{4}$ of the area of the square.
The pyramid's volume is $\frac{(2r)^2h}{3} = \frac{4r^2h}{3}$
So the cone's volume is $\frac{\pi}{4} \times \frac{4r^2h}{3} = \frac{\pi r^2 h}{3}$.
Non-square-based pyramids
We can use the same principles to find the volume of any pyramid.
Rectangular-based pyramid
If we have a pyramid with rectangular base measuring $a$ by $b$, and height $h$, then this can be obtained by stretching our square-based pyramid by scale factor $\frac{b}{a}$. The new volume will be $\frac{b}{a} \times \frac{a^2 h}{3} = \frac{a b h}{3}$.
Triangular-based pyramid
If the base of the pyramid is a triangle with base $a$ and perpendicular height $b$, it will fit exactly in the rectangular pyramid above.
Any slice will look like this:
Although we don't know the measurements of the rectangle in this slice, the sides will still be in the ratio $a:b$ (this may take some thinking about). Let's call them $k{a}$ and $k{b}$ (where $k$ is less than 1).
Area of rectangle = $k{a} \times k{b} = k^2 a{b}$
Area of triangle = $\frac{1}{2}{k}{a} \times {k}{b} = \frac{1}{2}k^2{a}{b} = \frac{1}{2} \times \mbox{area of rectangle}$.
If each triangle is half the size of the rectangle, the volume of the triangular-based pyramid will be half the volume of the rectangular-based pyramid, or $a{b}h/6$.
Generalisation
The formula for the volume of any pyramid is $\frac{1}{3}\mbox{base area} \times \mbox{height}$.Verify that this works for the pyramids above (and indeed for the cone). Can you convince yourself that this is always true?
