Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Published 2001 Revised 2012
Squareo'scope Determines the Kind of Triangle
Here are some experiments in which you can make discoveries about geometry.
Stage 1
You need about six thin straight sticks or thin drinking straws. Cut one into 3 bits. Can the bits form a triangle? It is not always possible to make a triangle using three given lengths. Experiment with sticks or straws of different lengths and try to find the condition which determines when three lengths do form a triangle and when they do not. This condition is called the Triangle Inequality .
Stage 2
You now need square paper bits (laminated ones preferably) ranging from 1 x 1 to 13 x 13 squares. Ideally the squares should be plain on one side and have squares marked on the other side.
Instead of using sticks, make triangles with the edges of three square bits of your choice using the plain sides. Every time you make a triangle, identify whether it is acute, obtuse or right angled and fill in the first column in the table.
Recall that a triangle is acute when each of its angles is less than a right angle or square corner. A triangle is right angled when one of its angles is a right angle or a square corner. A triangle is obtuse when one of its angles is greater than a right angle or square corner.
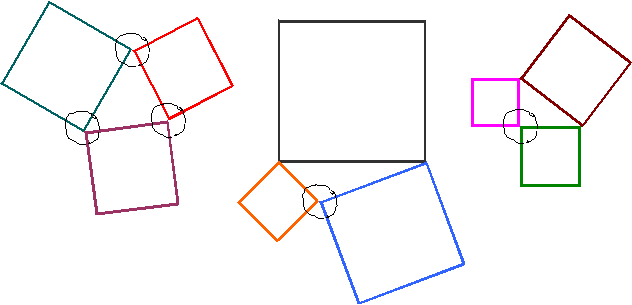
Sometimes you get acute angled triangles, sometimes right angled and sometime obtuse angled. Now turn over the squares showing the grids.
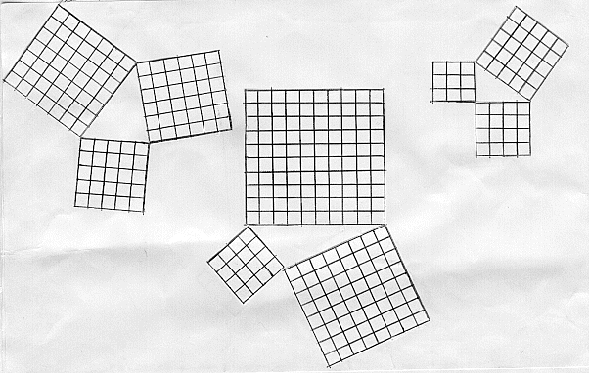
Use the paper squares to make different triangles. Fill in the table to help you to discover a test for deciding whether the triangle is acute angled, right angled or obtuse angled. In the last three columns fill in the box with < , = or > appropriately.
| Triangle number | Kind of triangle: acute, obtuse, right | Lengths of sides | Areas in square units | Relation between sum of two squares and the third square | ||||||
| a | b | c | a2 | b2 | c2 | a2 +b2  c2 c2 |
b2 +c2  a2 a2 |
c2 +a2  b2 b2 |
||
Stop and discover. Write down your discoveries. Do they agree with what is stated here?
- The Triangle Inequality : Three lengths form a triangle if and only if the sum of the lengths of any two of the three is greater than the third length. Equivalently as a single test, three lengths determine a triangle if and only if the sum of the two shortest lengths is longer than the longest of the sides.
- When the sum of the squares on two sides of a triangle is greater than the square on the third side, the same holds good for other pairs of sides as well, and the triangle is acute .
- When the sum of the squares on two sides of a triangle is equal to the square on the third side, then the triangle is right angled .
- When the sum of the squares on two sides of a triangle is less than the square on the third side, then the triangle is obtuse angled .
Take off
- Continue the exploration when the triangles are isosceles or equilateral.
- Without doing practical work, can you identify the kind of triangle from the side lengths given?
- 20,16,12
- 14,12,22
- 8,11,13
- 4,5.5,6.5
- 30,40,50
- 10,11,12
- How will you decide if a particular angle in a triangle with sides of given length is acute, right or obtuse without drawing the triangle?

