Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Coordinate Cunning
Age 7 to 11
Challenge Level 





- Game
This is a game for two players.
You will need:
A blue pencil and a red pencil.
A sheet of dotted paper.
The aim:
To get four dots of your colour in a line.
To play:
Together, decide where to place the origin (0,0). It can be on any of the points on the board.

Next, choose who will be blue and who will be red.
Blue goes first and chooses a point. Blue has to write down the coordinates of the point in relation to the origin. If they get the coordinates of the point wrong, they don't get that point.
What are the coordinates of the point that Blue has chosen here?
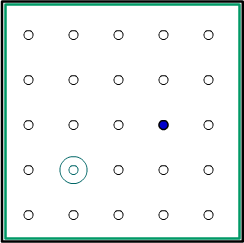
Then Red chooses a point and gives its coordinates.
Keep playing until one person has four dots in line of their colour!

