Give me four clues
Problem
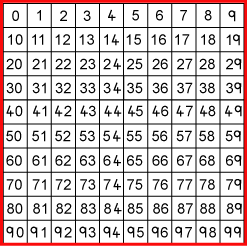
I am thinking of a number between 1 and 100. What's my number?
Look at the eight clues below.
Can you sort out the four clues that enable you to deduce my number?
Which four clues are not necessary, even though they are true?
Clues:
- The number is greater than $9$.
- The number is not a multiple of $10$.
- The number is a multiple of $7$.
- The number is odd.
- The number is not a multiple of $11$.
- The number is less than $200$.
- Its ones digit is larger than its tens digit.
- Its tens digit is odd.
Challenge:
Choose your own secret number between 1 and 100.
Write exactly four clues so that your friend needs each of them to guess your number.
Try it out on your friend.
Remember, avoid clues that double-up and therefore are not needed such as both 'it's even' and 'it's in the 4 times table'. Your four clues must lead to just one number between 1 and 100.
Getting Started
You could print off this sheet of the problem and mark or shade the grid somehow.
Which clue can you immediately see is not needed?
Which clue gives you the same information as the last two clues?
Student Solutions
We received lots of good solutions to this problem, so thank you to everybody who sent in their ideas. We haven't yet received any sets of your own clues, as in the second part of the problem, so please do email us to let us know if you have worked on your own version of this task.
Holly from Sacred Heart School in New Zealand told us:
The answer is 35
* statement 1 does not help because by following the other clues you can tell that you need more than 1 digit to find the answer and the only multiple of 7 smaller than 9 is 7, which consists of only 1 digit.
* statement 2 does not help because the ones digit has to be larger than the tens digit and the only multiple of 7 and 10 is 70 and the 0 is smaller than the 7
* statement 3 helps because being a multiple of 7 cancels out a lot of numbers that could have been possibilities.
* statement 4 helps because by being an odd number it too cancels out a lot of other possibilities
* statement 5 does not help because the only multiple of 7 and 11 is 77 and the ones digit has to be bigger than the tens digit and the two digits in 77 are even (even meaning the same).
* statement 6 does not help because you can only choose the numbers from 1-100, and those numbers are all below 200 anyway, so that statement is completely worthless.
* statement 7 helps because by using it there will only be a few numbers left to choose from.
* statement 8 helps because by using it you can easily narrow the number down so that there is only one left.
The only number left after using all of the useful clues is 35
Children at St Faith's School worked together and sent us the following solution:
The rules you need (in order) are:
- The number is odd (so cross out all the columns of even numbers). This is the most important rule because you can get rid of half of the numbers very quickly.
- The tens digit is odd (so cross out all the rows that have even tens numbers. These are 0-9; 20-29; 40-49; 60-69 and 80-89). We decided that all the numbers in the row 0-9 counted as numbers with an even tens number as the tens numbers in this row all equal zero and if we say that an even number is one which doesn't leave a remainder when you divide by 2 then zero counts as an even number. This
rule is important because it helps us cross out 25 more numbers.
- The number is a multiple of 7 (so cross out all numbers that are not in the seven times table). There are now only three numbers left: 35, 77 and 91.
- Its ones digit is larger than its tens digit (so cross out all numbers that have a number in the ones (units) column the same as or less than the number in the tens). This rule lets you cross out two of the remaining three numbers to leave the correct answer.
This leaves the number 35 so 35 is the correct answer.
The rules we didn't need were:
- The number is less than 200: you don't need this rule because all the numbers are less than 200 already so none would get crossed out!
- The number is greater than 9: you don't need this rule because numbers 0-9 have zero tens and all these numbers get crossed out later in the problem when you cross out all the numbers that have an even number in the tens.
- The number is not a multiple of ten: you don't need this rule because you have already crossed out all the multiples of tens when you crossed out all the even numbers.
- The number is not a multiple of 11: you don't need this rule because at the end when there are three numbers left (35, 77 and 91) if you used this rule you would only cross out 77 and still have two numbers left and need to use a 5th rule to choose between them so it is better for the last rule to be 'Its ones digit is larger than its tens digit' as this gets rid of two numbers and leaves the
right answer.
Cong also explained clearly how he went about the problem:
The number is 35. The way I worked it out is:
Thank you in particular to Vasil from Slivern in Bulgaria, Isobel from Springfield Primary, Alex and Leonor who also sent us clear solutions.
Teachers' Resources
Why do this problem?
Possible approach
Suggest that pairs continue to work on the problem, recording whatever and however they find useful. Let them know that you will be asking them to explain their reasoning, as opposed to simply focusing on the answer.
As you go round the room, listen out for children who are using logical reasoning to eliminate the redundant clues and to find the number. They might well use vocabulary such as 'because' and/or 'if ... then ...'. You could warn a few pairs that you'd like them to share what they have been saying with the whole group in due course.
Bring everyone together again to share their solution but in particular to share examples of logical reasoning that led to it. You can then set the group off on the follow-up challenge where they could work in pairs to create a similar task for another pair with exactly four clues, none of which are superfluous.
To end the lesson, place learners in groups of four so two pairs can try out each other's new challenges and report back.
Key questions
Possible extension
Possible support
