Name That Graph
Problem
Take a look at the parabola below.
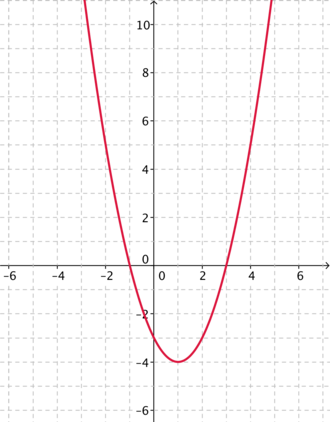
Can you find an equation for this parabola?
- In how many ways can you choose to show this equation?
- Which format did you initially choose and why?
What is the same and what is different about your approach to finding an equation of the two parabolas below, compared to the example above?
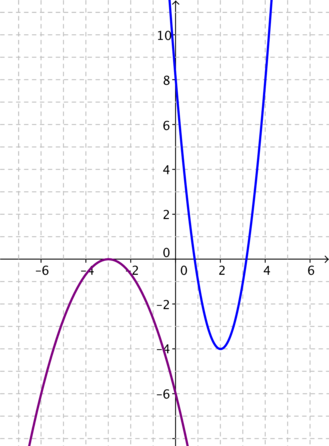
- What properties do the three parabolas have in common?
- Is there an approach to finding the equation that works for all three of these parabolas, and indeed for any parabola you could be given?
- Which approach to finding the equation was the most efficient? Is it the same approach for each example?
Underground Mathematics is hosted by Cambridge Mathematics. The project was originally funded by a grant from the UK Department for Education to provide free web-based resources that support the teaching and learning of post-16 mathematics.
Visit the site at undergroundmathematics.org to find more resources, which also offer suggestions, solutions and teacher notes to help with their use in the classroom.
Student Solutions
Sameer from Hymers College in the UK described a method for finding the equation of the curves:
Just from looking at the graph I know it is a quadratic graph, this means it contains an $x^2.$ The two forms of this [equation] are expanded and factorised.
An expanded formula looks like this: $y = x^2 -3x -4$
However solving a quadratic graph requires the factorised formula.
In order to factorise an equation, you need to look for two numbers.
In the equation $x^2 -3x - 4 = 0,$ the two numbers must add together to form $-3$ and multiply together to form $-4.$ These numbers are $1$ and $-4.$
The equation will look like this: $(x+1)(x-4) = 0.$
It has two solutions, this is because one of the brackets must equal $0.$
$x + 1 = 0$ or $x - 4 =0$ $\Rightarrow$ $x = -1$ or $x = 4$
Therefore $y=0$ when $x = -1$ or $x = 4,$ so the graph passes through $-1$ and $4$ on the x axis. These are the roots.
Sameer and Sam from England used this idea to find the equation of the first graph. Sam wrote:
The curve crosses the x axis at $3$ and $-1.$ So $x= -1,3.$ $(x+1)(x-3)$ because at least one of the brackets has to equal $0.$ When you multiply out the brackets you get the equation [$y=$]$x^2-2x-3.$
Sergio from Kings College Alicante in Spain used another method to check this answer:
This is Sergio's work for the second graph:
Anna got a different equation for the second graph. Anna's method is similar to the method Sergio used to check the equation of the first graph. Here is Anna's work:
The minimum point of the graph is when $x=2,$ therefore $y=a(x-2)^2+k.$
$y=-4$ when $x=2$ therefore $k=-4.$
When $x=0,$ $y=8$ because the y-intercept is $8.$ Therefore $8=a\times(-2)^2-4 = 4a-4$ and so $a=3.$
So the equation is $y=3(x-2)^2-4.$
Check when $y=0:$
$\begin{align}3(x-2)^2-4&=0 \\ 3(x-2)^2 &= 4\\ (x-2)^2 &= \dfrac43 \\ x-2&=\pm\dfrac{2}{\sqrt3} \\ x&=2\pm\dfrac{2}{\sqrt3}\end{align}$
$2+\dfrac{2}{\sqrt3}\approx3.15$ and $2-\dfrac{2}{\sqrt3}\approx0.85$ which looks about right.
Can you see why Anna and Sergio got different answers? Whose answer do you think is right?
This is Sameer's work for the third graph:
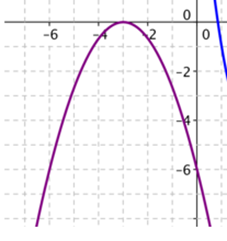
In this graph, the line is upside down compared to the others; this is because the $x^2$ is negative. The root is $-3,$ so the only solution is $-3.$
$x = -3$ or $x = -3$
$x + 3 = 0 or x + 3 = 0$
$(x+3)(x+3) = 0$
However, the $x^2$ is negative so one $x$ needs to be negative. This has to be the $x$ in the bracket with a $3$ so that the $3$ also becomes negative.
$-(x+3)(x+3) = 0.$
The expanded form is $-x^2 -6x -9$
Sergio added:
We need a y-intercept at $-6,$ not at $-9,$ so we multiply everything by $\dfrac{-6}{-9}=\dfrac23$:
$y=-\frac23x^2 -4x -6$

