Picture the process I
How does the temperature of a cup of tea behave over time? What is the radius of a spherical balloon as it is inflated? What is the distance fallen by a parachutist after jumping out of a plane? After sketching graphs for these and other real-world processes, you are offered a selection of equations to match to these graphs and processes.
Problem

This resource is from Underground Mathematics.
Here are descriptions of eight real-world processes. For each, try to sketch a suitable graph. If you are not familiar with the background science, then try to use what you do know to reason through what a graph might look like.
You do not need to calculate or plot exact points, just sketch graphs that give the general shape.
As you produce your sketches, make a list of the features that you are considering.
You can download Printable versions of these cards
| Temperature of a cup of tea over time. | Height of the valve on a bicycle tyre as the bicycle moves forwards. |
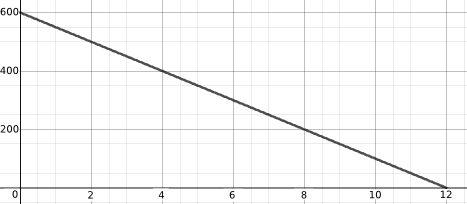
| Height of a tennis ball thrown straight up and then caught. | Distance fallen by a parachutist jumping out of a plane. |
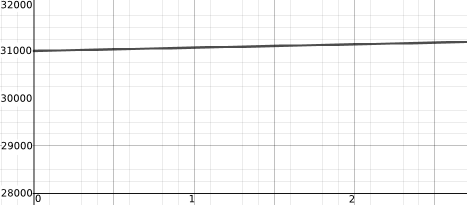
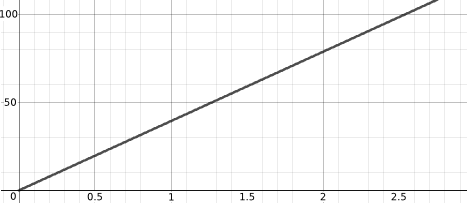
| Reading on the odometer (mile counter) of a car driving on a motorway. | Radius of a spherical balloon as it is inflated. |
| Volume of water remaining in a cup as water is sucked out through a straw. | Distance along a tape measure measured in inches compared with distance measured in metres. |
Once you have sketched graphs for some of the eight processes described, click on the following link to read a further question and move on further.
Underground Mathematics is hosted by Cambridge Mathematics. The project was originally funded by a grant from the UK Department for Education to provide free web-based resources that support the teaching and learning of post-16 mathematics.
Visit the site at undergroundmathematics.org to find more resources, which also offer suggestions, solutions and teacher notes to help with their use in the classroom.
Student Solutions
Weida from Churston Ferrers Grammar School has given very thorough explanations for why some of the physical processes have the equations and the graphs that they do, and has also interpreted what the numbers on the graphs mean in terms of physical quantities.
Radius of a spherical balloon as it is inflated
We assume that the balloon is being inflated at a constant rate i.e. the volume of the balloon increases steadily with time.
Let $V$ be the volume of the balloon, $t$ the time elapsed since we started inflating the ballon and $r$ the radius of the balloon. From the assumption, $ V \propto t$. Also we know that the volume of a sphere is given by $V = \frac{4}{3} \pi r^3$ so $V \propto r^3$. Therefore $ t \propto r^3$ so for some constant $A$
$$ r = A \sqrt[3]{t} $$

The equation given that matches this is $y(x) = 0.62043 \sqrt[3]{x}$.
Let us consider what the constant $A=0.62043$ represents. In $V \propto t$, the constant of proportionality is the volume of air put into the ballon per unit time, let's call this $p$. So
$V = p t = \frac{4}{3} \pi r^3 = \frac{4}{3} \pi A^3 t $
So $ p = \frac{4}{3} \pi A^3 = \frac{4}{3} \pi (0.62043)^3 = 1.00$ (3sf).
After 4 units of time on the graph the radius = 1 unit. So perhaps the units of time are seconds and 1 unit = 5 cm for the radius, in which case this would mean that every second $1 \times 5^3 = 125 \text{cm}^3$ of air was put into the balloon.
Height of the valve on a bicycle tyre as the tyre moves forwards
We assume that the wheel rotates at a constant rate, and that the bicylce is travelling horizontally. As the bicycle travels forwards, if we ignore the linear mostion of the valve in the direction that the bicycle is travelling, the valve is essentially tracing out a circle (see the sketch below)

Let $V=(x,y)$ be the position of the valve. When $V$ has turned through an angle of $\theta$ anticlockwise from the x-axis, looking at the right-angled triangle drawn, we see that $y=r \sin{\theta}$.
Thinking back to the bicycle, y is the height of the valve above the height of the centre of the tyre, and $r$ is the radius of the tyre. We may wish to convert the height above the centre of the tyre $y$ to the height of the valve above the ground $H$, by adding $r$.
Also as the speed is constant we can say that $\theta = k t$ where $k$ is some constant and $t$ is time. Combining this we have that
$$ H = r \sin{k t} + r $$

The given equtaion that this matches is $y(x) = 0.325 (\sin (3.1 x) +1)$. Comparing with $H =r \sin{k t} + r$ we see that $r=0.325$. As this represents the radius of the tyre, the unit is likely to be metres.
Can anyone see where the constant $3.1$ comes from if the x-axis represents distance the bicycle has travelled rather than time (and the angle is in radians)?
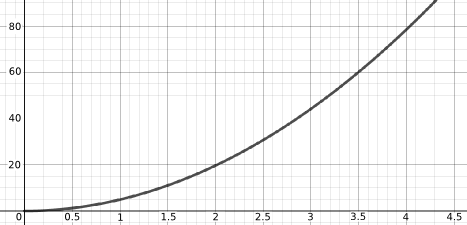
Temperature of a cup of tea over time
We assume that the rate at which the temperature decreases is proportional to the difference in temperature between the cup of tea and the room. So if $T$ represents the temperature of the tea and $t$ represents time, and room temperature is $20^{\circ}C$, then $-\frac{dT}{dt} \propto (T-20)$. This means, approximately, that the higher the temperature the faster the temperature decreases. On a graph of T against t, for smaller values of t, the gradient would be steeper.
From this we may set up a differential equation and solve it to find temperature as a function of time:
$$-\frac{dT}{dt} = k (T-20)$$
where $k$ is some positive constant.
Separating the variables we have
$$\frac{1}{T-20} \frac{dT}{dt} = -k $$
Integrating with respect to t,
$$ \int \frac{1}{T-20} \mathrm{d}T = \int -k \mathrm{d}t $$
$$ \ln{(T-20)} = -k t + c$$
Changing to exponential notation
$$T = 20 + e^{-k t + c} = 20 +A e^{-kt}$$
where $A$ is some constant.

The equation given that matches this is $ y(x) = 20 + 80 e^{-0.05 x} $. The units of temperature for the y-axis was probably degrees celcius implying that the tea starts at $100^{\circ}C$ and ends up eventually at $20^{\circ}C$. It is likely that the unit for $x$ is minutes because after 30 minutes it is likely that the temperature would be $y(x) = 20 + 80 e^{-0.05 \times 30} \approx 38^{\circ}C$
Can anyone explain the graphs and equations behind any of the other processes?