Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Completing Quadrilaterals
Age 11 to 14
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Special Cases
How do you define a rectangle? There are lots of possible definitions, such as:
A quadrilateral with four right angles.
Does a square satisfy this definition?
Answer: yes!
This means that a square is a special type of rectangle: it meets all of the criteria for a rectangle but has other special properties. Take a look at these rectangles:

One of these is special, and is given the extra name of a square, but it is still a rectangle. It is a special case of a rectangle.
Notice that all squares are rectangles, but not all rectangles are squares. Think about the right-hand rectangle above.
Here are some other examples of special cases:

These are a collection of rhombuses, one of which is also a square.

These are a collection of kites, one of which is also a rhombus.

This is a collection of parallelograms, one of which is also a rectangle.
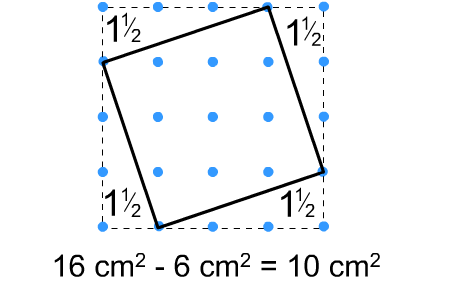
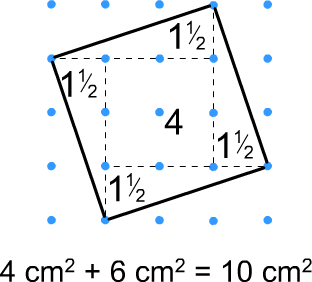
Two standard methods for working out the areas of tilted squares, which may help to work out the areas of the quadrilaterals:
Splitting the tilted square into right-angled triangles and squares and adding the areas of the different parts:
Boxing in the square, working out the area of the box and subtracting the areas of the unwanted right-angled triangles: