Making a difference
How many different differences can you make?
Problem
Making a Difference printable worksheet
There are a number of ways the digits $2, 5, 7, 8$ can be placed in a subtraction sum like the one below:
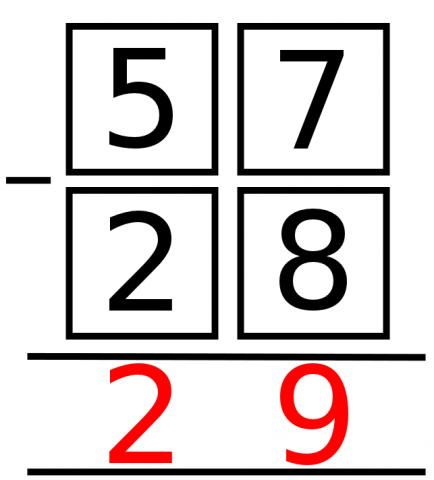
In this example, the answer is 29.
Can you rearrange the four digits to find all the (positive) answers it is possible to make?
Here are two follow-up questions you might like to consider:
- Can you work out which four digits you need to start with to be able to get all the possible answers $7, 9, 11, 13, 18, 22, 29$ and $31$?
- Can you show that, if we're only allowed to use consecutive digits (e.g. $5, 6, 7, 8$), $31$ is the largest possible answer and $7$ is the smallest?
With thanks to Don Steward, whose ideas formed the basis of this problem.
Getting Started
Here is one more example using 2, 5, 7 and 8:
82 - 75 = 7
Student Solutions
There were lots of good solutions to this question. Well done and thank you to everyone who submitted solutions! We couldn't include everyone's solutions, as there were too many, but well done to you all.
A number of you, including Fraser, Jacque, Dan and Jack, all from the Crypt School; Brendon and Ava, both from St Mary's Catholic High School; Lois, Jack, Oliver and Lewis from Kingsway Primary School; Hasan from Dixons Kings Academy and Sophie from Wallington High School for Girls found a number of the solutions, and many of them found all 12:
$\begin{eqnarray}
82-75 &=& 7\\
85-72 &=& 13\\
72-58 &=& 14\\
82-57 &=& 25\\
78-52 &=& 26\\
57-28 &=& 29\\
58-27 &=& 31\\
87-52 &=& 35\\
75-28 &=& 47\\
78-25 &=& 53\\
85-27 &=& 58\\
87-25 &=& 62
\end{eqnarray}$
Lev, from the Assosciated Hebrew Schools Danilack, Canada, was able to explain how he started finding these systematically, by looking at all of those numbers where the tens digit of the top number is $8$, which gave him six subtractions.
Ella, from Maidstone Girls Grammar School, and Mr Dutton's Maths Group, from Hartley Primary Academy, both explained how they managed to find all twelve solutions in a systematic manner. Here is Ella's solution
In order to find the solution to this problem, I worked systematically. First of all, I worked out all the possible sums if your first digit of the bigger number was five, then I did the same with seven, then eight. I didn't try it with two because all the other numbers possible would be bigger than any possible with the number two and then you would get a negative number, which wouldn't work.
Seth, from the British International School of Boston, USA, had a different systematic method:
To solve the puzzle 'Making a Difference' I first thought about the numbers there were to subtract from. I arrived at the answer : 25, 27, 28, 57, 58, 52, 72, 75, 78, 82, 85, and 87. But, if you look at the number which is composed of just the two smallest numbers or the numbers which have 2 at the start, and check the combinations for the subtracted number, you will find that all combinations from that are negative. After that, you can just try all other combinations and you're done!
Jamie, from Shrewsbury International School in Thailand, used a different method to systematically find the solutions.
There are 4 numbers. In the first square, you are able to put 4 different numbers. Keep the 4. The second square can have 3 different numbers, since one number is already used. There are two numbers that can go into the third square. And the last square matches with the last number left. Multiplying $4 \times 3 \times 2 \times 1 = 24$ gives the number of orders. This is also called $4$ factorial, written as $4!$.
Zach was able to develop this to get to again show that there are 12 solutions:
$4!$ gives 24 possible 4-digit numbers. These then form the two 2-digit numbers, but since the answer must be positive, $28$ and $57$ gives the same sum as $57$ and $28$. This means that half the possible 24 combinations are duplicates, as you always have to take the smaller number from the bigger number to get a positive result.
Max and Ben, from St. Columba's Primary School, Australia both found that 3, 4, 5 and 6 work to give the stated set of numbers.
$\begin{eqnarray}
53-46 &=& 7\\
63-54 = 45-36 &=& 9\\
64-53 = 46-35 &=& 11\\
56-43 &=& 13\\
63-45 = 54-36 &=& 18\\
65-43 = 56-34 &=& 22\\
64-35 &=& 29\\
65-34 &=& 31
\end{eqnarray}$
Jessica, from Wallington High School for Girls, was able to explain why any set of four consecutive numbers would give this set of answers.
The simplest idea I could think of to start with, was to use consecutive numbers. I realised that it didn't matter what consecutive numbers I used because the differences would cancel out. For example, using 1, 2, 3 and 4, 43 - 21 = 22. Using 5, 6, 7 and 8, 87 - 65 = 22. So when I tried 1, 2, 3, and 4, and crossed out all the negative answers, I got: 7, 9, 11, 13, 18, 22, 29 and 31.
Matty, Neo and Sienna, from the British School Manila, in the Philippines, Zach, Chris from Lakeside High School, USA, and Tomas from Wilson's School all used algebra to solve the final part. Here is a combination of their solutions:
For consecutive numbers where $a>b>c>d$:
$a = b+1$, $b = c+1$ and $c = d+1$.
Therefore $a=d+3$, $b=d+2$ and $c=d+1$.
For the largest gap, the tens digit of the top number must be as large as possible, and the tens digit must be as small as possible. This means the subtraction is $ab-cd$ (where $ab$ is the number with digits $a$ and $b$, rather than $a \times b$).
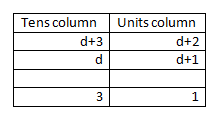
The largest difference is therefore 31.
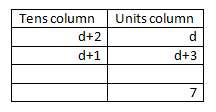
For the smallest gap it is $bd - ca$ because $a$ must be at the bottom because it is the biggest and you want to be taking away big numbers. It can't go in the bottom tens column because then the answer would be negative. b, the second biggest, can't accompany a because then it would also be a negative. c is the next biggest. This works out as positive.
Therefore the sum is:
Thank you again to everyone who submitted a solution, and well done!
Teachers' Resources
Why do this problem?
This problem offers students an opportunity to practise subtraction while challenging them to work systematically and think strategically.
Possible approach
This printable worksheet may be useful: Making a Difference.
Invite the students to draw a set of boxes like the ones below.

"Place the digits 2, 5, 7 and 8 into the four boxes, in whichever order you like, and then work out the answer to the subtraction."
Go round the room and invite students to share some of the differences they got.
"It seems like there's quite a few different ways to do it - I wonder how many different differences it's possible to make?"
You may wish to hand out this worksheet for students to record their working.
As the class are working, circulate and listen for useful observations from students, such as systematic ways of working to make sure they don't miss any possibilities.
Before students tackle the two questions at the bottom of the sheet, invite students to share any strategies that might be useful.
The final question about consecutive digits offers a nice opportunity for some discussion involving justification and proof.
Key questions
How do you know you've found every possible difference?
Possible support
The subtraction task in Dicey Operations might be a good initial activity for students who find column subtraction difficult.
Possible extension
Another task requiring students to work systematically to find all solutions is Weights.
