Vectors Round a Square
This resource is part of "Dotty Grids - Exploring Coordinates and Vectors"
Here is a diagram showing how vectors can describe a journey round a square:
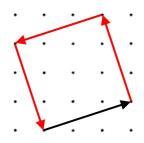
The journey starts along the black vector $\pmatrix{3\cr 1}$
What vectors describe the rest of the journey?
There are many interesting mathematical questions about vectors that describe journeys.
Explore journeys round various squares of your own and see what you can find out.
If you would like some ideas of interesting questions to explore, take a look below.
What happens if I add vectors together?
What is special about opposite sides of the squares?
What is special about adjacent sides of the squares?
If I know the vector for the diagonal can I work out the other vectors?
What about other shapes?
You may also like
Pair Sums
Five numbers added together in pairs produce: 0, 2, 4, 4, 6, 8, 9, 11, 13, 15 What are the five numbers?
Summing Consecutive Numbers
15 = 7 + 8 and 10 = 1 + 2 + 3 + 4. Can you say which numbers can be expressed as the sum of two or more consecutive integers?
Big Powers
Three people chose this as a favourite problem. It is the sort of problem that needs thinking time - but once the connection is made it gives access to many similar ideas.