You may also like
Some(?) of the Parts
A circle touches the lines OA, OB and AB where OA and OB are perpendicular. Show that the diameter of the circle is equal to the perimeter of the triangle
Polycircles
Show that for any triangle it is always possible to construct 3 touching circles with centres at the vertices. Is it possible to construct touching circles centred at the vertices of any polygon?
Circumspection
M is any point on the line AB. Squares of side length AM and MB are constructed and their circumcircles intersect at P (and M). Prove that the lines AD and BE produced pass through P.
Age 11 to 16
Challenge Level
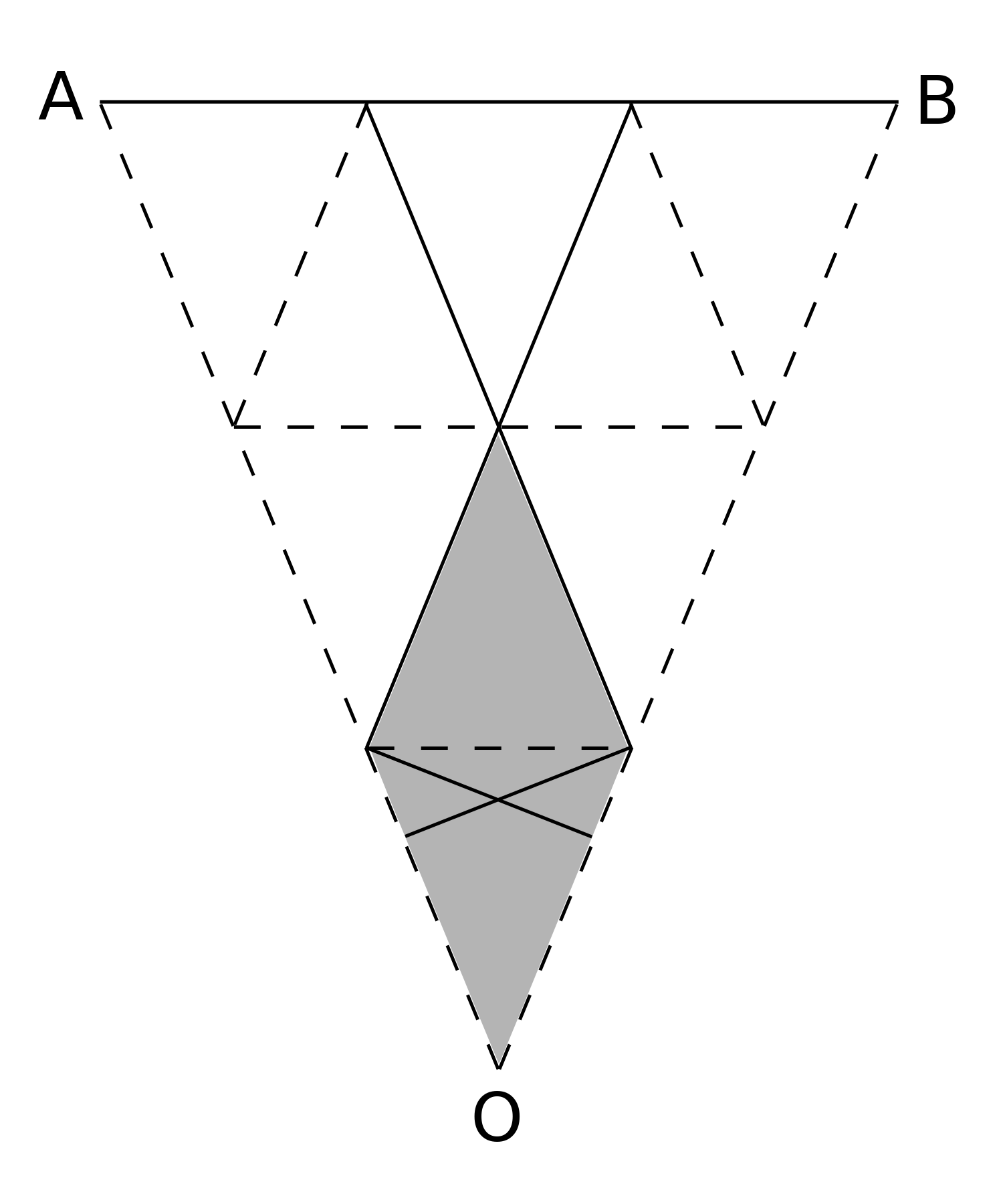
The diagram shows part of the ceramic. $A$ and $B$ are vertices of the outer octagon, which has $O$ at its centre. The lines $OA$, $OB$, two lines which are parallel to $AB$ and lines parallel to $OA$ and $OB$ respectively have been added. As can be seen, these lines divide $\triangle OAB$ into nine congruent triangles.
The shaded portion of triangle has area equal to that of two of the smaller triangles. So $\frac{2}{9}$ of the area of $\triangle OAB$ has been shaded. Now, the area of the outer octagon is eight times the area of $\triangle OAB$ and the area of shaded portion of the design is eight times the area of the shaded portion of $\triangle OAB$. Therefore, the fraction of the octagon which is shaded is also $\frac{2}{9}$.
Copyright © 1997 - 2023. University of Cambridge.
All rights reserved.
NRICH is part of the family of activities in the Millennium Mathematics Project.
NRICH is part of the family of activities in the Millennium Mathematics Project.