NRICH was delighted to work with Haringey Council again on a five-term project from January 2014 to July 2015. The project, funded by the London Schools' Excellence Fund, aimed to improve primary teachers' Maths subject knowledge and pedagogic knowledge, thereby increasing pupil attainment.
Liz Woodham, one of the NRICH Primary Coordinators, led the project with Michael Hall, an independent consultant and part-time lecturer at the Open University, who has worked with Liz on previous projects in Haringey.
Two primary teachers from each of approximately twenty schools in Haringey attended ten face-to-face sessions. This page is intended to be an information-sharing point.
Day 1: Thursday 6 February 2014
AgendaDay1.docx
Haringey Day 1 2014.ppt
We played Totality all together and discussed the mathematics we used, and its 'low threshold high ceiling' nature.
We spent some time considering what mathematical topics need to be focused on in each school. Here are the flipchart sheets which we created in this session:





Michael referred to a report 'Development of Maths Capabilities and Confidence in Primary School' by Nunes, Bryant, Silva and Barros (2009) which you can download here.
Another very interesting read is EffectiveTeachersofNumeracy.pdf. We didn't make reference to this report today, but are likely to do so throughout the project.
Michael also referred to this article in Primary Mathematics (published by The Mathematical Association) which is about a previous project between NRICH and Haringey.
Michael led us in the 'Flipping Cards' activity. There are five cards, each with a number on the front and another number on the back, like this:
Five participants stood up and flipped the cards until a mix of odd and even numbers were displayed. Without seeing the numbers displayed, Michael asked how many are odd and then announced the total of the five numbers. He repeated this several times.
The challenge is to explain how he knew the total.
The mathematical themes we discussed are:
- Maths is magical
- Maths is not about performing tricks
- The magic of maths is understanding the structure, design and presentation of the activity.
- People maths - the participants become the mathematics (numbers in this case)
(The activity is described in the I Hate Mathematics Book by Marilyn Burns, published by CUP, ISBN: 0521336597. A group of teachers Michael worked with some while ago devised the people maths presentation for the activity.)
Expectations for day 2 (19 March)
- complete maths audit in back of 'Mathematics for Primary and Early Years: Developing Subject Knowledge' book by Heather Cooke (see SelfAssessmentPrompts.docx for more details) and please bring score (count subsections of questions as being worth one mark each)
- ask each child in your class to complete the pupil questionnaire
- try out a rich task with your class and be prepared to chat about how it went
- you may wish to begin a learning log to record interesting moments that you notice in your classroom (brief extracts of what children say are worth noting for reflection and discussion).
Day 2: Wednesday 19 March 2014
AgendaDay2.docx
HaringeyDay2.ppt
During the day the tasks we tried all focused on developing children's number sense and understanding of place value. They can all be found in the Number Sense and Place Value Feature.
Liz mentioned research by Kenneth Ruthven which suggests a model for teaching mathematics: exploration -> codification -> consolidation, rather than a 'show then practice' model found in some mathematics lessons. Although the context is secondary mathematics, this feels very relevant for primary too. You can read the paper, published in Educational Studies in Mathematics
20 (1989) here: ExploratoryTeachingKRuthven.pdf.
We spent some time sharing our experiences of trying an activity out in the classroom. Here are the resulting flipchart sheets produced by each group:
As the above image is rather difficult to read, the text is in this document too.




We had a brief discussion about the completed pupil questionnaires, which Michael and Liz collected and we also talked about what it had been like doing the subject audit.
Expectations for day 3 (20 May)
- read chapters 5 and 9 of Listening Counts and identify a couple of children to focus on. (The reason for selecting them in particular is completely up to you e.g. they say very little; they are girls and you suspect they are underperfoming; they are high attaining but find application of knowledge difficult - it could be anything!). Begin to jot down observations and thoughts about
these children in your learning log.
- try out a rich task with your class and be prepared to chat about how it went.
Day 3: Tuesday 20 May 2014
AgendaDay3.docx
HaringeyDay3.ppt
Day 3 focused on recording mathematics. We had a go at School Fair Necklaces and used this activity as a springboard from which to discuss working systematically as well as aspects of recording.
Liz drew attention to the Recording Feature on NRICH, which includes an article outlining three different contexts for recording:
- Recording 'in the moment'
- Recording as thinking
- Recording for a different person/time
Later in the day, we tried The Amazing Splitting Plant, which lends itself to a variety of different ways of recording.
Emma and Marie from Bounds Green very kindly brought some of their children's maths books to share with us, which contain plain white pages rather than squares. We discussed the pros (e.g. freedom to record in any way children like) and cons (e.g. some cutting and sticking needed when task does need other types of paper). Emma/Marie were very enthusiastic about the books.
We spent a short time reflecting on how the project might be impacting on teachers and learners so far. Here are some of the comments made (paraphrased by Liz!):
- It's encouraging participatiing teachers to think more openly and use more open-ended questioning
- One school has given the same challenge to each class (using NRICH posters) once a week, and invited individuals/pairs/groups/classes to give in solutions; they are already seeing an improvement in number of responses and a wider spread of children contributing, although there is a challenge in helping other colleagues to maximise the potential of the tasks
- It's helped participating teachers consider how to scaffold tasks using appropriate questions
- It's encouraging participating teachers to think about how children are grouped for tasks
- The more open-ended tasks allow children to show their thinking
- Children are appreciating more mathematical freedom and the opportunities for more mathematical conversations
- Children seem to enjoy the tasks - why?
- Children see the games as fun and are less inhibited
We discussed chapters 5 and 9 of 'Listening Counts' and how reading them made us feel. It was suggested that chapter 5 could be worth sharing with colleagues back at school. We recognised that many teachers feel the pressure of 'coverage'. Could whispers be written on post-its? One participant described how she uses pupils as 'learning detectives' - a couple volunteer
(or are chosen) to listen in on conversations as others work on maths and report back.
Michael mentioned Mike Askew's article Private Talk Public Conversation which offers suggestions for effective paired talk and advice about making the most of whole-class discussion 'to build on methods that children have shared privately, refine the mathematics and reach a greater collective understanding'. (Here is a
link to a keynote speech by Professor Mike Askew at the joint HMIE/LTS Good Practice conference for mathematics held in the Carnegie Conference Centre in Dunfermline on 2 September 2009, which discusses similar ideas:
http://www.educationscotland.gov.uk/video/m/video_tcm4571623.asp.)[I'm sorry to report that that link is at present corrupt and will not work!]
Michael also led us in a deconstruction of a KS2 mathematics SATs question. Participants were grouped in fours with one card each (or in pairs with two cards each), each card giving some of the information from the question. Participants can say what is written on their card(s) but not show what is written. The challenge is to answer the SATs question 'How much change does Mrs
Patel get?' You can download the cards here: MrsPatelCards.doc
The idea is then to devise a similar set of cards with a different question to be answered.
Here are the mathematical themes which emerged in discussion:
- Questions with surplus or missing data.
- Talk not see
- Small group work
- Generating own mathematical questions
(This was adapted from an idea in The Numeracy File, written by Mike Askew and Sheila Ebbutt, published by Nelson Thorne.)
Expectations for day 4 (3 July)
- read chapter 4 of 'Listening Counts' and note points which you would particularly like to share
- continue to add to your Learning Log
- try out at least one more rich task with your class
Day 4: Thursday 3 July 2014
AgendaDay4.docx
HaringeyDay4.ppt
We focused on fractions today. We began with a discussion about why children might find fractions so difficult. Ideas included:
- abstract nature
- not much link to everyday life
- difficult vocabulary
- can be counter-intuitive (e.g. one quarter is smaller than one third even though, when considering the denominators, 4 is bigger than 3)
- need to know tables
- hard to visualise
- link to whole (which could be ANYTHING!)
- equivalence is a difficult concept
Liz drew attention to the article Understanding Fractions which suggests the reasons are:
- relative rather than fixed amount
- same fraction might refer to different quantities and different fractions may be equivalent (what is the whole?)
- can refer to objects, quantities or shapes
(See ppt presentation linked above for more detail.)
Liz shared a ppt animation focusing on halving, featured in the teachers' resources section of Halving, and we then tried the task itself. We also had a go at Fair Feast. One participant described using this problem with her Year 2 class very successfully. She had intended it as a short task, but it ended up taking quite a bit of time as
the children were engrossed and didn't find it quite as straightforward as she'd anticipated. Liz flagged up the Fractions Feature on NRICH which contains the article mentioned above as well as the activities and more.
Michael and Liz drew attention to the progression charts on the NCETM website (you need to be logged in to view them). We also shared the fractions part of a spreadsheet copiled by the ATM and MA which also indicates progression and displays the content in terms of sub-topics. Here is the full spreadsheet: Overview by topic of the NC 2013.xlsx
We spent some time composing reflections on the project so far, which were sent to Michael/Liz.
The next session began with Michael writing the following on the board:
$\frac{2}{3} + \frac{4}{7} = \frac{6}{10}$
Our reaction was that the calculation was incorrect. Michael then explained that he was recording the fact that in his first test he had got 2 out of 3 questions right and in the second test he had got 4 out of 7 correct. So, in total he had got 6 out of the 10 questions right. We reflected on this ...
Michael then led us in some paper folding which linked well to the Halving animation in the first session. We created a square from an A4 piece of paper, then folded in half and half again, and half again ... We unfolded after each stage to count the triangles we had created.
Michael then read us an extract from a Paddington Bear story in which Paddington is answering questions for a TV quiz show:
"If”, he said, “you had a piece of wood eight feet long and you cut it in half, and if you cut the two pieces you then have in half again, and if you then cut all the pieces into half again how many pieces would you have?”
“Eight” said Paddington promptly.
“Very good, bear,” said Ronnie Playfair approvingly.
“Here is the second part of the question. How long will each of the pieces be?”
“Eight feet” said Paddington almost before the Master of Ceremonies had time to start the clock. “Eight feet?” repeated Ronnie Playfair “You're sure you won't change your mind?”
“No, thank you, Mr Playfair, “said Paddington firmly.
“In that case ... I must ask you for the £5 back, the answer is one foot”.
“Oh no, Mr Playfair” said Paddington politely “I'm sure that's right for your piece of wood but I cut mine the other way.”
“But if you're asked to cut a plank of wood in half,” stuttered Ronnie Playfair, “you cut it across the middle not down the middle. It stands to reason.”
“Not if you're a bear,” said Paddington, remembering his efforts at carpentry in the past.
“If you're a bear it's safer to cut down the middle.”
Bond, M., 1971 Paddington at Large: Collins, London.
'Doing a Paddington' can therefore be thought of as us listening to our learners and really trying to understand their logic. It also challenged us to think about what makes a good question and what makes a good answer. (The idea for this activity came from an article by Prestage and Perks in Mathematics in Schools Volume 21, Number 4, a journal published by The Mathematical
Association in September 1992.)
With A4 paper we folded as Paddington did and cut one strip out to fold the 'other' way. Then we asked, 'what if the strip is one metre in length?' and so on. With a second strip we tried folding into three equal parts and discussed why it is more difficult and how it generalised folding into n parts. Finally, we linked to mental calculation and finding fractions of an amount by asking what
length of strip would suit three folds and n folds.
Finally we used another strip which we assumed to be 36cm in length and rolled two dice to find fractions of 36. Discussion centered on how to work out the fractions that seemed difficult and why they were difficult.
Later in the day, we spent some time discussing chapter 4 of 'Listening Counts' and began to think about outline plans for a staff meeting back at school in the autumn.
Michael led two more mathematical activities. The first of which started with the description of a dad who was cutting a cake in half to share between his two children. The question is, did he actually cut it in half? What fractions might he have created? This led to trying to state fractions nearer and nearer to a half which weren't a half exactly.
Michael also reminded us of the counting stick and how it can be used to count in fractions and links with decimals - great for chanting and mental work.
In the second activity, Michael gave out cards with a fraction or percentage on each. Participants had to line up to order their cards. Those participants who didn't have a card were then asked to choose a fraction/percentage between two already on the number line and everyone had to work out what their fraction/percentage was through questioning.
Adell from Earlsmead mentioned the story 'The Greedy Triangle' which developed into an investigation around regular polygons (using straws and pipe cleaners), lines of symmetry and lots of areas that were unexpected. If you're interested, here is the link: http://www.youtube.com/watch?v=kPuI4XyyZUE
Expectations for day 5 (9 October)
- read chapter 7 of 'Listening Counts'
- continue to try out rich tasks with your class
- mull over ideas for the staff meeting
- take a look at the Problem Solving feature on NRICH, particularly the articles
Day 5: Thursday 9 October 2014
AgendaDay5.docx
EmbeddingThreeAims.ppt
HaringeyDay5.ppt
We welcomed some new participants today and also Lynne McClure, the Director of NRICH, who led the day, which was entitled 'Embedding The Three Aims of the New National Curriculum'. See Lynne's PowerPoint slides, linked above.
Session 1 focused on supporting reasoning and fluency through rich tasks. We began by having a go at Reach 100, followed by Strike It Out. Lynne talked about wanting to confuse children (not permanently!) as the work to get 'unconfused' is where the learning takes place. We discussed the 'low threshold high ceiling' nature
of Strike It Out and the two versions:
1. Competitive with an addition/subtraction focus (could use numicon, number cards, cards with 'add', 'take away' etc written on, could have an adult recording for a child)
2. Collaborative - this could then become a 'simmering' activity which goes on beyond the length of the lesson, which gives a strong message that maths doesn't just take place in lesson-sized chunks and models the behaviour of mathematicians.
We talked about tweaking the number line to include multiples of ten, decimals, fractions, negative numbers etc.
Lynne outlined some relevant research and the idea that children need to have both procedural fluency and conceptual fluency.
We looked at how we the collaborative version of Strike It Out could be used as a vehicle to develop logical proof - can we use all the numbers on the number line? (We decided we couldn't use 0 but discussed the benefit of having 0 included as a 'red herring'.)
Lynne summarised two types of reasoning - inductive and deductive (see her ppt above for details).
In session 2, Lynne focused on problem solving. She gaves us bags of dominoes and asked, "How do you know you've got all them all?" (See the NRICH task Domino Sets.) Different groups arranged the dominoes in different ways to try to answer this question:




Lynne then challenged us with Amy's Dominoes, some groups were allowed to keep the dominoes, some had to return them to the bag. We discussed how important the initial 'playing around' with the dominoes had been before tackling this task and the implications on how we allow children to choose structured apparatus in the classroom. Lynne mentioned Ruthven's
research: Exploration > Codification > Consolidation (see Day 2 details above for more info).
Lynne introduced us to sets of houses (used in Guess the Houses) and again, asked whether we thought we had a full set.
We used the domino sets to have a go at Guess the Dominoes, a group task, and talked about the ways you could make this more accessible (see teachers' resources section of the activity).
Session 3 was a split session, with Liz leading an information gathering session for the majority of participants (see PowerPoint linked at top of this section 'HaringeyDay5'), and Lynne leading a session with the Haringey Maths Working Party.
Session 4 focused on mathematical games. We played the following games and reflected on their mathematical content, how they could be adapted/extended and how they contributed to fluency, reasoning and problem solving:
Dotty Six
Board Block
Four Go
Some Games That May Be Nice or Nasty
Stop the Clock
Got It
We discussed how an element of strategy always increases the level of thinking required and sometimes if the mathematical content of a game is low, it can free children up to reason in a more sophisticated way. Lynne drew attention to the fact that these games have huge potential and can be returned to again and again, rather than being 'one-off' activities in the classroom.
Expectations for day 6 (11 November)
- Those of you who have been with us since January, please email Michael (copied into this message) with the average point score of your last year's class, plus the average point score of a class in that same year group the previous academic year. This is urgent! Please email Michael by next Tuesday (21st).
- Please try out at least one of the tasks we had a go at on Thursday with your class and be prepared to share your experiences next time we meet.
- Please ask all the pupils in your current class to complete the PupilQuestionnaire and bring the copies with you next time.
- Those of you new to the project and who have already been given a copy of the 'Mathematics for Primary and Early Years' book, please have a go at the assessment in the back and bring your score with you next time (assuming each part of a question is worth one 'point').
Day 6: Tuesday 11 November 2014
AgendaDay6.docx
HaringeyDay6.ppt
Michael started the day by sharing some of the data collected through the project so far - see ppt file above. He thanked everyone for their high quality participation which had resulted in such impressive achievements already.
Today focused on geometry. Michael began session 1 by asking everyone what the word 'geometry' made them think of. Answers included:
- logarithms,
- helping children with the range of vocab in terms of names of shapes
- different children often excel in this area compared with number/calculation
- link with Art
Michael led a brief 'people maths' activity, asking one person to come to the front to represent a dot, a second person then represented a line being drawn. How do we make this 2D? 3D?
Michael then drew a horizontal line near the foot of the flipchart paper (asking "What's this?"), then a vertical one near the left edge so it intersected with the horizontal line, creating a pair of axes. He asked someone to mark a point. The question was then, "What are the coordinates of the point?". This prompted discussion about scale. The point was given coordinates,
then Michael asked, "If that point is the corner of a square, what are the coordinates of the other corners?". This led to "Can you tell from four sets of coordinates whether the shape will be a square?" and "If I gave you two coordinates, can you give me the other two which make a square?". (See the problem Square Coordinates.)
We discussed the open nature of this line of questioning. Some children may find that rather daunting at first so you could have cut-out squares for them to use on a grid. However, the openness gives learners ownership of the task/s, involves them and encourages them to visualise. The activity necessitates thinking relationally about coordinates (i.e. how does this pair of
coordinates relate to that one?), which can lead to generality. Michael suggested that 'geometry' is about the relationship between things whereas 'shape and space' tends to be thought of as labels for shapes.
The first session finished with a challenge that is commonly given to Year 7 students in Hungary: '(1, 3) is a vertex of an isosceles triangle. If it has an area of 9 cm$^2$, where are the other two vertices?'. (See here for an almost identical NRICH problem, also aimed at Key Stage 3 students.)
Michael asked how we were feeling. Responses included:
- it was helpful to talk through this task (the triangle one), I couldn't have done it on my own
- we used trial and error, firstly by drawing an isosceles triangle (on squared paper), finding the area then adjusting the area to make 9 cm$^2$
- we found it difficult - we drew a triangle first, then found the area, then put in the coordinates.
Michael concluded by drawing attention to Holt's suggestions of what it means to understand (taken from 'How Children Fail', first published in 1964 by Penguin). The points were generally thought to be helpful and we agreed to try them out with children. (OpeningOutCoordinates.ppt summarises this first session.)
Liz led the second session which drew on ideas in Jennie Pennant's article Developing Excellence in Problem Solving with Young Learners. See the HaringeyDay6.ppt also linked at the top of this day's section. Jennie suggests that there are three main ways in which we can help learners become
confident and competent problem solvers:
- Through choice of task
- Through structuring stages of the problem-solving process
- Through explicitly and repeatedly providing children with opportunities to develop key problem-solving skills.
We had a go at Poly Plug Rectangles and discussed what makes it a rich task. Suggestions included:
- everyone can succeed but it can be extended easily
- great for strategic thinking
- opportunities for reasoning
- opportunties for visualising.
Liz shared NRICH's thinking about the four stages of the problem-solving process (see Jennie's article and/or ppt above), and we considered what we might observe children doing at each of the stages in the context of Poly Plug Rectangles. We discussed the problem-solving skills we had used to tackle the task and how we might make sure, as a school, that children have experience of all the
main skills. Liz drew attention to the fact that of course this task also offers opportunities to develop reasoning and fluency, the focus of the other two aims of the new NC (in conjunction with problem solving). The fluency is interesting here as it is not number/calculation focused. Liz showed the Teachers' Resources section of Poly Plug Rectangles,
which includes some video of Lynne and Liz working on the problem with a class of Year 2 children.
Liz reminded everyone of the Problem Solving Feature and the curriculum mapping documents on the NRICH site.
Session 3 gave everyone chance to share what they had tried out with children since last time. The following posters were created as we reflected on experiences: 





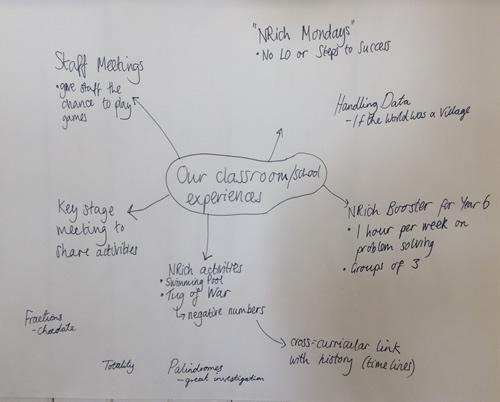
Session 4 began with some people maths. Michael invited everyone to make a rectangle. He asked, "What size rectangle have you made?" [6 by 10 with two people forming each corner]; "How many people are there?" [32] and "How do you know?". We numbered round to check the total. Then "Who's in the corner?". Michael was surprised at this outcome as he did
not expect two teachers in each corner of their rectangle. With one teacher in each corner, the perimeter would have been 36 teacher units with only 32 teachers in the room. The conflict being that the corner teachers are counted twice. By putting two teachers in each corner the group seemed to have anticipated this conflict!
Then, Michael asked everyone to make a rectangle where we were all the rows and columns too. (At this point there were 33 participants.) Then the challenge was to make another one, which we did by turning to face a different direction. This is a great representation of an array and in particular of 33 being both 11x3 and 3x11.
The mathematics could then be taken into factors, arrays, multiples ... The same mathematics could be done with interlocking cubes on tables (not the same number on each table so they generate different examples). You could ask children to make some shapes, make some rectangles ...
We discussed how people maths can provoke a different sort of engagement with ideas. (The Association of Teachers of Mathematics, ATM, have produced two people maths books: People Maths Hidden Depths and More People More Maths.)
Michael then led a serious of visualisation tasks:
- Picture a 3x5 rectangle. What's its area? What's its perimeter? (Michael then showed one made from large squares.) Now remove 1 square from the border. What's the area now? What's the perimeter? Michael encouraged us to articulate why the area/perimeter had changed or had remained the same. Can we take any other squares away and keep the perimeter the same? And now? And now?
- Using geostrips, Michael created a rectangle and then 'slid' the sides to create a parallelogram. He asked what's the same, what's different? He did a similar thing to a square, creating a rhombus.
- Michael held up a triangle and asked what the angles added up to [180$^\circ$]. He then opened out another triangle to create a quadrilateral. What do the angles add up to now? [180$^\circ$ x 2 = 360$^\circ$]. He then opened out another triangle to create a pentagon. What do the angles add up to now? [180$^\circ$ x 3 = 540$^\circ$]. He then opened out another triangle to create a hexagon. What do the angles add up to now? [180$^\circ$ x 4 = 720$^\circ$]. Pattern and generality with the 360 times table! Here is the resulting shape:

Session 5 allowed participants to plan for work back in school and to discuss running a staff meeting with colleagues. Liz reminded participants about the wealth of articles on the NRICH site which help planning for progression in various topics. They can be accessed via the search or our list of CPD articles for the classroom.
In session 6, Michael led some more visualisation tasks:
- Imagine a large equilateral triangle in your head. Paint the triangle using white paint. You have three smaller triangles which are all black. Pick up one, place it in one of the three corners. Pick up a second one and place it in one of the other two corners. Finally, place the third triangle in the last corner. What is the white shape? What do you see? This ppt presentation includes these ideas.
We chatted about how we felt about this visualisation and the conversations led to talking about 'upsidedown' triangles!
Michael made an equilateral triangle out of geostrips and we discussed the fact that a triangle is rigid so can't be 'slid'. This has applications in the construction industry.
Michael posed more questions:
- He asked everyone to picture a cube and put a dab of paint on one vertex. How many edges have got paint at one end? Go to the other end of one of these edges and put another blob of paint on that vertex. How many edges have paint at one end now? How many edges don't have any paint at either end?
- If there are four beetles/birds in a tree and they are equidistant from each other, what would their positions be? [tetrahedron]
- Hold a piece of A4 paper in portrait position. Fold the bottom right corner to meet the longer side on the left. (This creates a right angled triangle which is half of a square together with a rectangle above. How do you know there is a square?) Then fold the top right corner to meet the nearest side of the folded right angled triangle - what shape do you have now? [kite]

We spent a short time considering how we know that the angles of a triangle add up to 180$^\circ$. Michael asked all participants to bring back next time ways of exploring this with children. We discussed how triangles drawn on the surface of a sphere do not have angles that total 180$^\circ$. One participant gave the example of two lines of longitude meeting at the north pole
at 90$^\circ$ but also crossing the equator at 90$^\circ$.
At the very end of the day, Liz showed this presentation which loops round. Here are some notes about it, written by its author. For further ideas, see Geoff Faux's article in the ATM journal, Mathematics Teaching, edition 205.
Expectations for day 7 (5 February)
- Please continue to try rich tasks with your class and be prepared to share your experiences next time we meet.
- Plan for a staff meeting in your school, or consider how you will follow up from the staff meeting/s already led.
- If you have not already done so, please ask all the pupils in your current class to complete the PupilQuestionnaire and bring the copies with you next time.
- Those of you new to the project and who have already been given a copy of the 'Mathematics for Primary and Early Years' book, please have a go at the assessment in the back and bring your score with you next time (assuming each part of a question is worth one 'point').
- Take some time to consider how you might explore the idea that the angles in a triangle add to 180$^\circ$.
In the meantime, don't forget there are lots of collections of geometry tasks suitable for Key Stages 1 and 2 if you scroll down the curriculum page of NRICH.
Day 7: Thursday 5 February 2015
AgendaDay7.docx
HaringeyDay7.ppt
This day focused on algebra. In Session 1, Michael led four different activities to get us thinking about algebra.
To begin, he asked us to imagine a drawer of socks which contained only two different types of socks. How many socks would you have to take out of the drawer to be sure of having a pair? How many would you have to take out if there were three different types? Four different types? Five ...? We were able to identify a pattern and express a generality: 'You need to
take out one more sock than you have types of socks'. We discussed how this is an example of algebraic thinking. You could use letters to express this thinking, but that might be an end product.
In his second activity, Michael asked us to list numbers that 'go into' 2015 exactly. We found:
1 and 2015
5 and 403
13 and 31
Michael introduced the concept of prime factors - any number can be uniquely described by the product of prime numbers so in this case 2015 = 5 x 13 x 31. Michael then asked us to take each prime fact (5/13/31), square it and add 1. We noticed that the result was always even. Why? Again, we were able to think algebraically by considering the generality:
odd x odd = odd
odd + 1 = even
Michael then asked us to think of a number and follow these instructions:
Double
Subtract 4
Halve
Take away the number you first thought of
We were always left with 1. Why? Michael then challenged us to develop our own 'think of a number' (THOAN) activity which would result in an answer of 2. This proved hard. One participant described looking for patterns, making conjectures but then finding that what they had tried didn't work. Another suggested simply taking Michael's THOAN and adding in a final instruction 'double your answer'! One participant suggested the following:
Add 3
Double
Take away 2
Halve
Subtract the number you first thought of
We found a way to explain why this always work, using a 'bag' in which we would place the number we first thought of: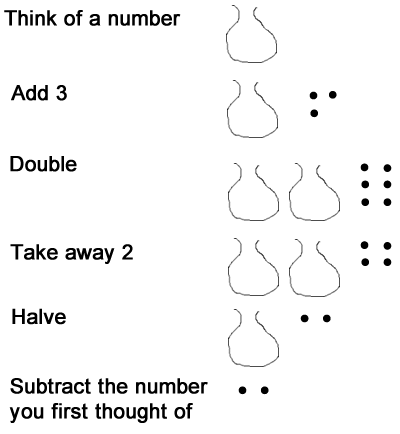
Michael's fourth activity was based on a 100 square. He asked us to choose a number on the square and then find three other numbers which made a 2 by 2 square with the first number. For example, I might choose 7. Then I could choose:
7 8
17 18
Michael asked us to add diagonal pairs and we discussed what happens. We found a way to explain why the diagonals always add to the same total:
| number | number + 1 |
| number + 10 | number + 11 |
Then the total of the diagonal from top left to bottom right = number + number + 11
The the total of the diagonal from bottom left to top right = number + 10 + number + 1 = number + number + 11
Michael suggested we could try finding the diagonal products too.
In session 2, Liz led us through a number of NRICH tasks which will help us embed algebraic ideas throughout the primary curriculum, rather than just at Year 6 where algebra is specifically mentioned (see the ppt file linked above). All the activities can be found in the Algebra in the New Curriculum Feature. We had a go at Number
Balance, which can help learners get to grips with the concept of equivalence and we discussed use of the equals sign, which should not be seen as an instruction ('makes'), but rather as meaning 'equivalent to'.
We discussed missing number problems and this led into Heads and Feet, which is an example of such a problem but it also encourages children to represent their mathematics in a whole range of ways. We tackled Shape Times Shape, which can be a good context in which to get children used to the idea of symbols representing numbers. Colour
Wheels, Ip Dip and Up and Down Staircases give learners opportunities to identify patterns and then generalise them.
Liz referred to Lynne's article Making Algebra Rich (contained in the feature linked above) which suggests that the roots of algebraic thinking are:
- balancing and the equals sign
- using symbols then letters
- generalising from a number of examples and stating a rule.
In session 3, we spent a short time sharing experiences of using rich tasks since we were last together. Key points included:
- Use of Fractional Wall activity helped children work systematically and use knowledge of equivalence and, for example, 'half a half'
- Used Three Dice, children worked in pairs and needed several attempts to find out that opposite sides of a dice add to 7.
- NRICH tasks had been used for homework, but they were perhaps too challenging so a workshop is being organised for parents to help them support their children
- Teacher confidence - using systematic approaches and modelling new problems
- NRICH advent calendar was useful for Y6 - they warmed up to problem solving!
- Books are an issue - pressure to present work beautifully; freedom for children to show their working; designated page/book for recording thoughts/solutions?
- Some activities are too hard
- Some of my colleagues still view NRICH as a 'fun' Friday afternoon thing
- Up, Down, Flying Around is an amazing way of letting children discover what happens when you add and subtract negative numbers and there are good extensions and modifications
- NRICH curriculum maps very helpful for planning purposes
- Loved Snail One Hundred with Y2 for tens and units
- Everybody in school using NRICH at least once a week
- Children need to be taught meaning of problem-solving strategies. What does visualisation mean? Needs to be explicit.
- Using an NRICH activity at the start of the week has been an effective way of scaffolding/extending learning for the rest of the week
- Giving greater ownership to children
- For Shapes Times Shape, you could box off starting points and next steps for the less confident
- Whole school policy to create group roles - NRICH activities lend themselves to this and encourage group work and collaborative work
- Using NRICH weekly allows collaborative work, good for allowing children to explain their reasoning
- Like using NRICH to embed fluency i.e. different activities allowing children to go deeper rather than rushing through
Session 4 was an opportunity for participants to suggest areas of the curriculum which they personally would like future sessions to focus on, or areas that were priorities for their school. The following came up, in order of preference:
- mental maths
- assessment (planning and progression)
- problem solving
- challenging SEN children
- challenging the gifted
- division (not chunking)
- word problems (especially money)
- ratio
- subtraction
- multiplication
- place value
In session 5, we looked in a bit more detail at the National Centre for Excellence in the Teaching of Mathematics website (NCETM), which requires registration. We navigated to the new National Curriculum resource tool and Michael gave an overview of the current Shanghai project, which involves Chinese and English teachers
of mathematics spending time in each other's classrooms (see ppt slides for summary and this interim report). NCETM has also published guidance on what makes a high quality Maths textbook.
In the final session of the day, after time for planning, Michael followed up some of the geometrical ideas we explored on day 6. We made a triangle from a piece of A5 paper, then held it so that one side was horizontal:
We found the midpoint of the other two sides by folding and joined these two midpoints by folding to create a line. We then folded down the 'top' corner of the triangle along that line so that it met the horizontal edge:
Finally, we folded the left and right corners in along a perpendicular to meet the first corner:
We discussed how this shows that the angles of a triangle add to 180$^\circ$.
With another piece of A5, we made a cylinder, discovering that two different cylinders could be made:

Michael asked whether the volumes of these cylinders are the same. How might we test? We could fill them with something (e.g. rice) or use a formula to help ...
Michael then 'magically' transformed a square into a circle:
The first question was 'what is the same and what is different about the square and the circle?'. This led to discussion about the words 'perimeter' and 'circumference' and to the area of the two shapes - were they the same? One suggestion was that they would not be the same because the use of pi would lead to decimals whereas the area square need only involve whole numbers.
Expectations for day 8 (17 March)
- Please continue to try rich tasks with your class and colleagues, and be prepared to share your experiences next time we meet.
- Lead a staff meeting in your school, or consider how you will follow up from the staff meeting/s already led.
- If you have not already done so, please ask all the pupils in your current class to complete the Pupil Questionnaire and bring the copies with you next time.
- If you have not already done so, please have a go at the assessment in the back of the 'Mathematics for Primary and Early Years' book, and bring your score with you next time (assuming each part of a question is worth one 'point').
In addition, you might like to take some time to explore the Algebra Feature on NRICH and the NCETM website.
Day 8: Tuesday 17 March
AgendaDay8.docx
HaringeyDay8.ppt
Today's tasks provided opportunties to use mental calculation strategies but we discussed them particularly from the point of view of encouraging children to reason mathematically.
In the first session, we tried two tasks from NRICH, Maze 100 and Mystery Matrix, and used them as a springboard to talk about when we reason. We thought that reasoning was necessary when:
- the starting point is not obvious
- we are deciding which skills to use to tackle the task
- we are evaluating solutions
- we are looking for alternative solutions
- we are drawing on prior knowledge.
We discussed what we do when we reason (see the PowerPoint presentation linked above) and then Liz shared NRICH's view of progression in reasoning, which consists of five stages:
- describing
- explaining
- convincing
- justifying
- proving
We had a go at Make 37 and then, in session 2, we discussed what each of the five stages of reasoning might 'look like' in the context of this task. Here are the resulting ideas:




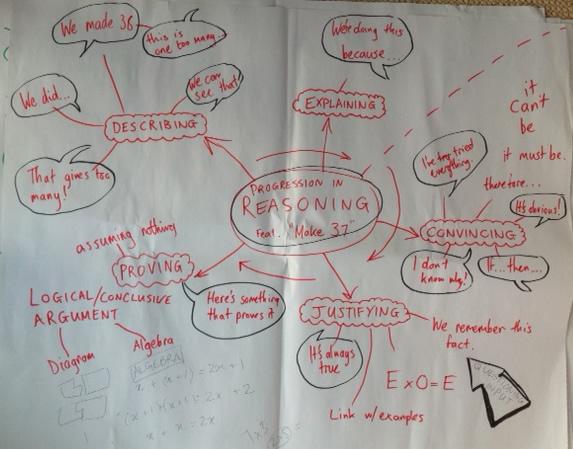

We discussed how to help children get better at reasoning by helping them move through the different stages. We reflected on the fact that quite often, when asked about their solutions to a task, children describe what they have done rather than offer explanation, let alone convince us, justify or prove. We thought it would be useful to
look for the possible generality in tasks so that we can support learners in reasoning at a higher level.
As a whole group, we considered what a proof of Make 37 could look like and Michael jotted down the following notes on the flipchart:
The idea of a picture proof (or visual proof, or iconic proof) seemed very powerful in this context and we felt we could use Multilink or Numicon or drawings as above. There is much more detail about the stages of reasoning in the article Reasoning: The Journey from Novice to Expert, which is part of NRICH's Reasoning Feature.
Michael requested class attainment data from each participating teacher and suggested it could be submitted to him as average point scores. The following templates might be useful:
APS blank.docx
YEAR FOUR APS sample.docx
Yr 3 class sample.xlsx
However, Michael encouraged everyone to pass on data in whatever format it is available and to also send data for the equivalent class from the previous academic year.
In session 3, we shared experiences of working on rich tasks with children since we last met. Points mentioned included:
- Modelling the problem-solving process using 'WAGOLL' (what a good one looks like)
- The desire that children be able to use visualisation
- Using task 'templates' such as same/different; always/sometimes/never true; odd one out
- Using a game to consolidate understanding with an added layer of strategy (how can I stop my partner from winning?), for example Stop the Clock and the Factors and Multiples Game
- Tackling problems in a group and assigning each child a role (see NRICH Developing Group-working Skills Feature)
- Making the language of problem solving explicit
- Valuing different approaches to the same task, for example role play/using concrete resources/drawing a picture to solve Andy's Marbles
After lunch, we had a brief discussion about progress with staff meetings and how the project might be affecting other colleagues beyond the face-to-face participants. Every school was asked to complete this form to summarise the current situation.
Following on from planning time, in the final session of the day Michael linked back to day 7 which had focused on algebra. He gave out number cards to some individuals and they had to put themselves in order and describe the pattern.
He then split the whole group into two. Each group was given twelve cards and asked to organise them into two separate sequences:


We ended up with a sequence that went up in threes:
2, 5, 8, 11, 14, 17
and the Fibonacci sequence:
1, 1, 2, 3, 5, 8
where each term is the sum of the previous two.
We discussed how we would generate the first sequence and generalised it as 'one less than a multiple of 3' or, as 3n-1 where n is the position of the term in the sequence e.g. the first term = 3x1 - 1 = 2; second term = 3x2 - 1 = 5 etc.
We talked about how counting forwards and backwards in different steps is a useful activity and this led to us trying to extend the Fibonacci sequence backwards:
1, 1, 2, 3, 5, 8
0, 1, 1, 2, 3, 5, 8
1, 0, 1, 1, 2, 3, 5, 8
-1, 1, 0, 1, 1, 2, 3, 5, 8
2, -1, 1, 0, 1, 1, 2, 3, 5, 8
-3, 2, -1, 1, 0, 1, 1, 2, 3, 5, 8
5, -3, 2, -1, 1, 0, 1, 1, 2, 3, 5, 8 etc. etc.
We noticed the symmetry around 0.
Michael demonstrated another task, called 'Guardian of the Rule' whereby a number was suggested and then he wrote down another number having applied a rule. For example:
7 -> 71
4 -> 41
3 -> 31 etc
Here the rule would be 'multiply by 10 and add 1'.
Michael then showed us another task, which started with a word and then generated a sequence of words, each one being the number of letters in the previous word, for example:
HARINGEY - EIGHT - FIVE - FOUR
We tried this out with our names and realised that you always end up with 'Four'. Why? We will follow this up next time.
Finally, the last task Michael led invited us to think of four consecutive whole numbers, to find the product of the middle two and the product of the outer two, then find the difference between these two products. We discovered you always get a difference of two. Why? We will also return to this challenge next time.
Expectations for day 9 (20 May)
- Please continue to try rich tasks with your class and colleagues, and be prepared to share your experiences next time we meet.
- Lead a staff meeting in your school, or consider how you will follow up from the staff meeting/s already led then please complete this form and return to Michael/Liz.
- Bring class data along as soon as you can or send it to Michael.
- Take a look at the Reasoning Feature on NRICH.
- Have a think about the last two challenges above and come to the session with some explanations and possibly proofs.
Day 9: Wednesday 20 May
AgendaDay9.docx
HaringeyDay9.ppt
This day focused on use of calculators. Michael introduced session 1 with a brief round-up of the history of the use of calculators in primary schools. The Calculator Aware Number Curriculum project took place in the eighties and the findings of that project suggested that calculator use didn't 'interfere' with the learning of calculation. The Cockcroft review
was very positive about the use of calculators. In the National Numeracy Strategy, they were suggested for use in later KS2 for calculating, but also with younger children as an aid to learning mathematical ideas effectively (see this article http://www.tes.co.uk/article.aspx?storycode=331380). On our
day, Michael and Liz focused on the use of the calculator in this latter context, to help children understand the structure of mathematics rather than as a tool to perform calculations for them.
In the first activity, Michael 'did something' to his calculator and he asked for suggestions as to numbers he could test so we could find out what it was, which produced the following:
17 --> 0.53125
32 --> 1
A similar activity can be done with multiplication as repeated addition by keying in, for example $ 6 + + $ to produce the six times table. If children are encouraged to say the result outloud before they press = it may increase motivation ("say and press"). You can also ask the class to create sequences going backwards, for example, if they start at 72, what would they need to press repeatedly to get down to 6? This links to the fundamental idea of an inverse operation ('undoing'). There was a comment that inputting number sentences (or the reverse of a number sentence given to you) into the calculator may help some chlldren with sequencing.
The second activity was a 'broken calculator' task. If the '6' is broken on your calculator, how could you work out the following:
48 x 6
146 divided by 7
3.6 + 1.4
126 - 78
product of 126 and 58
difference between 76 and 263
32 + 16
65 + 56
62 x 16?
This task produced many solutions to each part and provoked discussion about how it was differentiated easily. You could ask children to discuss strategies and which calculations are easier/harder. It could also lead into a discussion about which strategy might be most efficient (and what 'efficient' means e.g. as few steps as possible so reducing room for error). We concluded that there are endless possibilities with a broken calculator activity!
In the third activity, Michael asked us to choose four digits and make two two-digit numbers, then to find the product of these two numbers. Which combination of two-digit numbers creates the biggest product? We were left to think about this and Michael will follow it up next time. (Digit cards or place-value cards could be useful here if doing this in the classroom.)
In the fourth activity, Michael split us into two groups. One group was allowed to use the calculator, the other was not. Michael showed different calcuations in turn (written on large cards) and the first person to shout out the answer won a point for their team. The calculator team always had to key the full calculation into the calculator before answering. This could encourage discussion about when mental methods are more appropriate and when reaching for a calculator is more appropriate. We would hope children ask themselves "what's the best way to do this, given these numbers?" rather than sticking rigidly to a particular method, regardless of the numbers involved.
We briefly discussed how giving children lots of opportunities to 'play with' numbers really helps. For example, use the date - what do you know about the number 20? Some children will automtically challenge themselves so that others in the group 'bump into' ideas that they might not have otherwise come across.
The fifth activity challenged us to think of a four-digit number less than five. (There is an element of surprise just in doing that!) Then, the idea was to choose any operation to change it into a three-digit number. For example:
4.363 --> 4.363 + 0.007
1.235 --> 1.235 x 2
4.999 --> 4.999 + 111.001
This could provoke nice discussions about the number of zeros needed!
Michael's sixth activity was called 'Zap to Zero' (Michael read about this in the article 'Zap to Zero Revisited' by Prestage and Perks in Maths in School May 2004 Vol 33 Issue 3, p.25, published by The Mathematical Association). We put the number 63478219 into our calculators and the idea was to 'zap out' the smallest
digit first by performing a calculation. In this case it was 63478219 - 10. This left us with 63478209 and we then had to 'zap out' the 2 and so on until the number is reduced to zero. This is another easily tweaked task - the number of digits could be altered and a decimal point could be introduced. An alternative version could involve only zapping the ones digit using
subtraction and multiplication. For example:
63478219 x 0.1 = 6347821.9
6347821.9 - 1 = 6347820.9
6347820.9 x 0.1 = 634782.09 etc. etc. until the number is reduced to zero
In session 2, Liz shared several examples from NRICH which make use of a calculator to deepen understanding of mathematics (see ppt slides linked above) and we discussed how each task might help meet the aims of the new National Curriculum (problem solving, reasoning and fluency). Secret Number would be a good precursor to Michael's first activity
above. It encourages children to make the link between addition and subtraction as inverses of each other (fluency) and offers plenty of opportunities for reasoning - "I knew that your secret number was ... because ...".
Forgot the Numbers is a challenging task which has no obvious route to the solution and will help deepen children's understanding of the relationship between multiplication and division. We had chance to think about it for a few minutes and then Liz gave each table a set of cards which offered some children's different starting points for solving the task. The idea
was to take one example and follow it through to a full solution (this is detailed in the teachers' resources section of the task and you can find the cards there to print off too). This led to some rich discussion about the relative efficiency of different methods and how 'unpicking' other people's solutions is a good way to help improve the communication of your
own reasoning. Emma from Bounds Green shared her pictorial method for solving the task: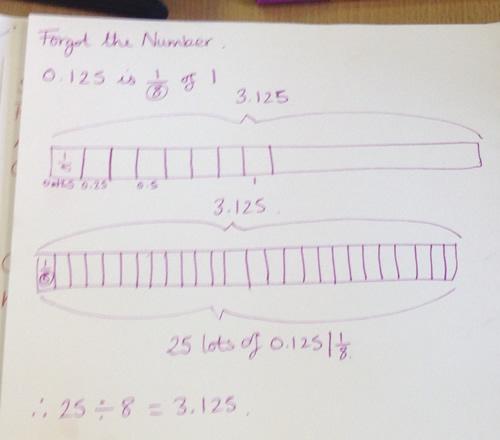
Session 3 gave us time to share experiences since last time. Here are photos of the flipchart sheets on which groups recorded their thoughts:



In the final session of the day, Michael returned to one of the tasks from last time in which he generated a sequence of words, each one being the number of letters in the previous word, for example:
HARINGEY - EIGHT - FIVE - FOUR
We tried this out starting with a word of our choice and realised that you always end up with 'Four'. It was suggested this is because 'four' is the only number word which contains the same number of letters as its name.
Michael also returned to the four consecutive numbers task from last time - write down four consecutive whole numbers, then find the product of the middle two and the product of the outer two, then find the difference between these two products. We discovered you always get a difference of two. We explained this together using a combination of algebraic and visual proof:
So, the product of the first and last is n x (n+3)
The product of the middle two is (n+1) x (n+2)
To help us work out these products, we could draw arrays:
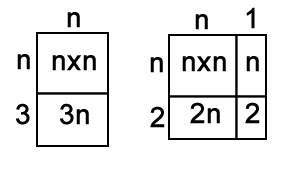
The left-hand array represents the product of the first and last consecutive numbers, so
n x (n+3) = nxn + 3n = n$^2$ + 3n
The right-hand array represents the products of the middle two consecutive numbers, so
(n+1) x (n+2) = (nxn) + 2n + n + 2 = (nxn) + 3n + 2 = n$^2$ + 3n + 2
So we know that the difference between the two products will always be 2.
To finish off the day, Michael posed two more calculator challenges. In his seventh activity, we were asked to type three digits into the calculator and then the same three digits again, for example 749749. Michael asked us to divide by 7, which surprised us as it produced a whole number for all of us. We then divided that answer by 11, which gave each of us another whole number; then by 13 to give the three-digit number we had started with. We tried to reason why this works ... Again, the idea of inverses was useful in this context. We multiplied 7 x 11 x 13, which gives 1001. Any three-digit number multiplied by 1001 gives a six-digit number with the first three digits repeated. So, if we start with a a six-digit number with the first three digits repeated and divide in turn by 7, 11 and 13, we will return to the three digit number.
Finally, the eighth activity involved choosing two numbers on the calculator which are next to each other but not diagonally next to each other. We had to make a two-digit number using those two numbers, and another two-digit number using the same numbers, for example 89 and 98. We were invited to find the difference between our two numbers. By pooling our results, we found that the difference is always a multiple of 9, why? Michael left us with the challenge of investigating what happens if you choose diagonally adjacent numbers.
Expectations for day 10 (2 July)
- Please continue to try rich tasks with your class and colleagues, and be prepared to share your experiences next time we meet.
- Lead a staff meeting in your school, or consider how you will follow up from the staff meeting/s already led then please complete this form and return to Michael/Liz.
- Bring class data along as soon as you can or send it to Michael.
- Please complete the subject audit in the back of the 'Mathematics for Primary and Early Years: Developing Subject Knowledge' book by Heather Cooke (for the second time) and bring your score (count subsections of questions as being worth one mark each).
- Please come prepared to talk about a 'significant moment' for you during the project. We will endeavour to capture these through video/audio recordings so if you have a tablet/smart phone which you don't minding using for that purpose please bring it too.
- Have a think about the two challenges above (third and eighth activities) and come to the session with some explanations and possibly proofs.
Day 10: Thursday 2 July
AgendaDay10.docx
HaringeyDay10.ppt
On the last day of the project we focused in general terms on embedding problem solving in the primary maths curriculum, drawing on content from the previous nine days. Liz and Michael gave out copies of this document which summarises the topics we have looked at over the course of the project as a whole.
In the first session, Liz drew attention to the following key issues which NRICH would suggest need to be considered in order for problem solving to be embedded in practice (see our Problem Solving Feature):
- Tasks
- Naming and drawing attention to problem-solving skills
- Structuring a problem solving lesson
- Types of problem
- Objectives
- Recording
- Classroom culture
We discussed key problem-solving skills:
- visualise
- work backwards
- reason logically
- conjecture
- work systematically
- look for a pattern
- trial and improvement
and how we might usefully break down the problem-solving process into four stages:
Stage 1: Getting started
Stage 2: Working on the problem
Stage 3: Going further
Stage 4: Concluding
We had a go at Five Steps to 50 and considered what made it a rich mathematical task, the problem-solving skills we used, how we could use it in the classroom, what the lesson objectives might be, how we might structure the lesson as well as what children might record and for what purpose.
We also had a few games of Dicey Operations (adapted so that we were adding two two-digit numbers to get as close as possible to 100 - see ppt slides) and discussed the reasoning it might elicit. We reminded ourselves of NRICH's suggested progression in reasoning (see day 8) and then tweaked Dicey Operations so that we threw the dice four times before
placing any digits and considered how we could prove that our arrangement produced the arrangement which was indeed closest to 100. Again, we discussed Dicey Operations generally in terms of the problem-solving skills used, structuring it in the classroom etc as with Five Steps to 50.
To end the first session, we had a go at Reasoned Rounding, and again discussed the task in terms of problem-solving skills used, structuring it in the classroom etc as with Five Steps to 50 and Dicey Operations.
In session 2, participants had chance to reflect on 'significant moments' during the project. These were recorded either in an audio/video format or in a Word document. Please send any further contributions to Michael and Liz.
Participants from one school described how their headteacher has been persuaded to integrate a problem-solving approach into maths teaching across the school from September, given the attainment data of the Year 1 classes, which have been trialling this approach through our project. They also described a trial with Year 3 in conjunction with the maths subject leader, whereby for one half
term, all maths was problem solving and no particular 'content knowledge' teaching sequences were planned, unless the need arose from a task. This teacher described the transformation in the children, who became much more resilient and confident learners of mathematics as a result.
In session 3, Michael led us in some fractions tasks. He began by asking us to list any four single digit numbers, not including zero. We were challenged to take two of our numbers and make a fraction, then another, then another ... How many different fractions would we be able to make? (16) (We discussed whether we were allowed the same number as both
numerator and denominator of a fraction and decided we were.) Groups wrote each fraction on a separate piece of paper and then were asked to order or organise them in some way. Here are some of those arrangements:


(This task is taken from 'Starting Points' by Banwell, Saunders and Tahta, published by OUP, ISBN 0 19 919009 7.)
Michael drew our attention to three articles, all published in Mathematics Teaching, the journal of the Association of Teachers of Mathematics:
Removing the Glass Ceiling on Mathematical Achievement in Primary Classrooms: Engaging All Pupils in Mathematical Learning by Sue Gifford and Penny Latham, Mathematics Teaching 232
Big Ideas: An Idea with Primary Potential? by Nancy Barclay and Alison Barnes, Mathematics Teaching 234
Mini-Theorems by Jonny Griffiths, also in Mathematics Teaching 234
In session 4, after lunch, participants were reminded about submitting the following to Michael/Liz please, before the end of term:
- pupil attainment data (for details see day 8 above)
- subject knowledge audit scores (contained in the back of 'Mathematics for Primary and Early Years: Developing Subject Knowledge' book by Heather Cooke'), assuming that subsections of questions are worth one mark each
- updated information about staff meeting/other CPD led in/beyond school.
After time for planning, Michael introduced another task in session 6: write down three single-digit numbers that add to zero. (This produced an element of surprise for some.) For example, participants offered:
-8, 4, 4
-5, 5, 0
5, -2, -3
4, 5, -9
We were then challenged to take two of our three numbers and create a fraction. How many are possible? (6) Michael then invited us to find out what happens when we:
- multiply all the fractions
- add all the fractions
This produced some perhaps surprising results!
Michael then returned to the eighth challenge he had posed last time, namely choosing two numbers on the calculator and creating two two-digit numbers from them, then finding their difference. For example, if I chose 5 and 6, the two two-digit numbers would be 56 and 65. Their difference is 9. Or, for 6 and 4, we end up with 64-46=18.
One participant conjectured that if the two numbers chosen were consecutive, we would always end up with a difference of 9. Here is the proof that was offered:
10n + (n+1) - [(n+1)10 + n]
= 10n + n + 1 - (10n + 10 + n)
= 11n + 1 - (11n + 10)
= 11n + 1 - 11n - 10
= -9
We took this a step further and created the following proof for any two digits, a and b:
10a + b - (10b + a)
= 9a - 9b
= 9(a-b)
So the 9 tells us it will be a multiple of 9 and the (a - b) tells us which multiple of 9. This means that the difference between the two two-digit numbers is 9 times the difference between the two digits!
At the end of the day, Michael and Liz thanked all participants for their commitment to the project as a whole. We looked forward to the conference on October 13, which will celebrate the project's achievements and begin to unpick some ideas associated with mastering mathematics in the context of problem solving.
Mastering Mathematics and the New Primary Curriculum
One-day conference, 13 October 2015
This conference aimed to celebrate the achivements of our five-term project and to look forward to the Leadership project which Michael and Liz will be running in 2015-16 in Haringey, within the context of 'mastery'.
The day comprised two keynotes, led by Professor MIke Askew and Lynne McClure, along with three workshops run by Haringey teachers, Michael and Liz. For more information about the day, please see this summary.
First published February 2014, last updated October 2015
