Find all the triples of numbers a, b, c such that each one of them plus the product of the other two is always 2.
Join the midpoints of a quadrilateral to get a new quadrilateral. What is special about it?
Take a triangular number, multiply it by 8 and add 1. What is special about your answer? Can you prove it?
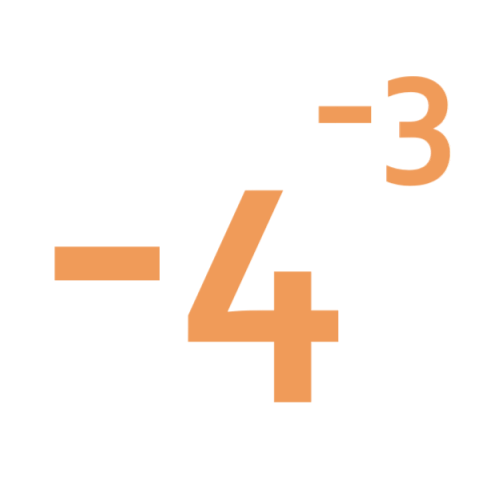
What does this number mean? Which order of 1, 2, 3 and 4 makes the highest value? Which makes the lowest?
10 graphs of experimental data are given. Can you use a spreadsheet to find algebraic graphs which match them closely, and thus discover the formulae most likely to govern the underlying processes?
If I tell you two sides of a right-angled triangle, you can easily work out the third. But what if the angle between the two sides is not a right angle?
Can you make sense of the three methods to work out what fraction of the total area is shaded?
This problem challenges you to find cubic equations which satisfy different conditions.
Show that if you add 1 to the product of four consecutive numbers the answer is ALWAYS a perfect square.
Which numbers cannot be written as the sum of two or more consecutive numbers?
