Copyright © University of Cambridge. All rights reserved.
'Striking Gold' printed from https://nrich.maths.org/
Show menu
This problem allows for a range of sophistications in calculation. The first stages are all about making rough approximations using the given approximation for the radius of the atom.
$r_A = 1.2 \times A^{\frac{1}{3}}$
$\Rightarrow r_A\ \propto \ A^{\frac{1}{3}}$
$\mathbf{\Rightarrow A\ \propto \ r_A ^3\ \propto \ Volume}$
The original expression makes sense since each time the atomic mass increases, the volume roughly increases by a set amount since ~ 1 proton and 1 neutron are added each time.
The radius of the alpha particle is calculated by recognising that an alpha particle is simply a helium nucleus. Therefore, it has an atomic number of 2, which can be substituted into the previously given formula:
$A_\alpha = 2$
$\mathbf{r_2 = 1.2\ \times\ 2^{\frac{1}{3}} = 1.51\ \text{fm}}$
The radius of the gold nucleus can be calculated by identifying that gold's atomic number is 79, and then substituting this into the given equation:
$A_{Au} = 79$
$\mathbf{r_{79} = 1.2\ \times\ 79^{\frac{1}{3}} = 5.15\ \text{fm}}$
This scatting parts of the problem allows for a range of sophistications in calculation. The first step is simply to assume that the alpha particle is a point mass:
Deflection only occurs if an alpha particle collides with the nucleus of the gold atom. The simplest approach to this part of the problem is to assume that the alpha particle is a point mass. This modelling assumption means that the probability of it being deflected by the gold atom is the ratio of gold atom's nuclear cross-sectional area to the total atomic cross-sectional area:
$$
\begin{align}
p\left(\textrm{deflection by gold atom}\right) &=\left({\frac{\textrm{Cross-sectional Area}_{nucleus}}{\textrm{Cross-sectional Area}_{atom}}}\right)
=\left({\frac{r_{nucleus}}{r_{atom}}}\right)^2\\
&=\left({\frac {5.15\ \times\ 10^{-15}}{135\ \times\ 10^{-12}}}\right)^2
= \mathbf{1.45\ \times\ 10^{-9}}\;.
\end{align}
$$
Parin and Matt continued to look at more detailed ways of considering the scattering of the alpha particles, starting with considering the possibility of glancing blows:
A slightly better approach to modelling the situation is not to assume that the alpha particle is a point mass, but to instead insist that it has physical dimensions. It can be reasoned that a deflection will now occur not just if there is a direct impact with the nucleus, but also due to a glancing blow if the alpha particle's centre of mass passes at a distance of $r_{nucleus}$ and $r_{nucleus} + r_{\alpha}$ of the centre of the gold nucleus. Thus, it can be thought that the gold atom's nucleus has an effective radius of $r_{nucleus} + r_{\alpha}$:
$$
\begin{align}
p\left(\textrm{deflection by gold atom}\right) &=\left({\frac{\textrm{Effective Cross-sectional Area}_{nucleus}}{\textrm{Cross-sectional Area}_{atom}}}\right) =\left({\frac{r_{nucleus}\ +\ {r_{\alpha}}}{r_{atom}}}\right)^2\\
&=\left({\frac {5.15\ \times\ 10^{-15} +1.51\ \times\ 10^{-15}}{135\ \times\ 10^{-12}}}\right)^2 = \mathbf{2.43\ \times\ 10^{-9}}\;.
\end{align}
$$
Note that this 'glancing blow' calculation assumes that particles behave like Newtonian billiard balls. In reality, the boundaries of the nuclei are somewhat blurred and the effects of quantum chemistry will need to be taken into account to develop a, so-called, effective scattering cross section.
The final part of this question can be tackled with varying degrees of assumptions. The simplest approach to the scenario is to assume that the alpha particle will pass through layers of gold atoms but that the probability of being stopped by each layer is independent of previous layers. Thus, by multiplying the probability of being stopped a layer by the number of layers, the total probability of deflection will be calculated. An additional assumption is that the gold particles have 100% efficient packing in the lattice.
$$
\begin{align}
n \times p\left(\textrm{deflection by one layer}\right) &= p\left(\textrm{deflection by gold sheet}\right)\\
n \times (2.43\ \times\ 10^{-9}) &= \frac{1}{8000}\\
\mathbf{n} &\mathbf{= 51346 = 51300\ layers\ (3\ s.f.)}
\end{align}
$$
using the more rigorous value of $p\left(\textrm{deflection by gold atom}\right)\;.$
A more rigorous approach to calculating the number of layers is as follows: let $\beta$ denote $p\left(\textrm{deflection by gold atom}\right)$. The probability that an alpha particle is deflected by the first layer is simply $\beta$; the probability that it is deflected by the second layer is conditional on it passing through the first layer, and is given by $(1-\beta)\beta$; the probability that it passes through the $n^{th}$ layer is $(1-\beta)^{n-1} \beta$. Therefore, the overall probability of deflection is:
$$ p\left(\textrm{deflection by whole sheet}\right) = \beta + (1-\beta)\beta + (1-\beta)^2 \beta + (1-\beta)^3 \beta + ... + (1-\beta)^{n-1} \beta\;.$$
This is a geometric series which gives:
$$
\begin{align}
p\left(\textrm{deflection by whole sheet}\right) &= 1- (1-\beta)^n\\
\therefore n &= \frac{\log\left(1-p\left(\textrm{deflection by whole sheet}\right)\right)}{\log(1-\beta)}\;.
\end{align}
$$
Using the rigorous value for $\beta$ gives:
$$\mathbf{n =51350 = 51400\ layers\ (3\ s.f.)}\;.$$
A further approach to calculating the number of layers is to realise that the gold atoms do not pack with 100% efficiency into the lattice, and that there is a degree of unfilled space. The formula calculated previously using $\beta$ is still applicable, but an adjusted value of $\beta$ must first be calculated.
The face of a unit cube of a gold lattice is shown below. By modelling the lattice such that each gold atom is as large as possible such that the gold atoms touch but overlap, the dimensions of the unit cube can be calculated as a function of the atomic radius.
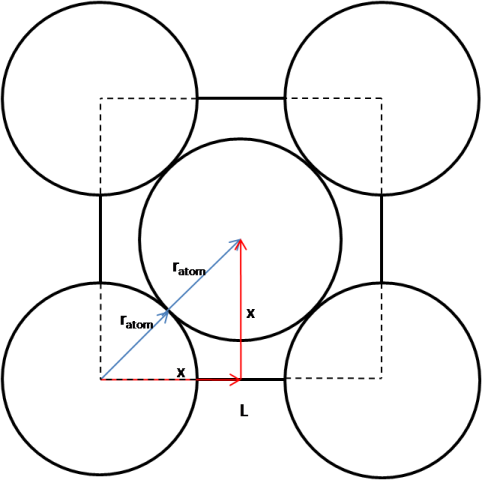
$x^2 + x^2 = (r_{atom} + r_{atom})^2$
$\rightarrow 2x^2 = 4r_{atom}^2$
$\therefore x = \sqrt{2} r_{atom}$
$\therefore L = 2x = 2\sqrt{2} r_{atom}$
$\textrm{Cross-sectional area} = 8 r_{atom}^2$
It should be noted additionally that each unit cube contains a total of 2 gold nuclei.
$\therefore \beta = \frac{2 \pi (r_{nucleus} + r_{\alpha}) ^2}{8r_{atom}^2} = \frac{\pi}{4} \left(\frac{r_{nucleus} + r_{\alpha}}{r_{atom}}\right)^2$
$\beta = \frac{\pi}{4} \left(\frac{(5.15 +1.51)\times 10^{-15}}{135 \times 10^{-12}}\right)^2= 1.91\ \times\ 10^{-9}$
$\mathbf{\therefore n = 65380= 65400\ layers\ (3\ s.f.)}$
Now, having used three methods of varying rigour to calculate the number of layers of gold atoms there are, the inter-layer spacing must now be calculated in order to ascertain what the thickness of the gold sheet is.
From the previous diagram of the unit cube, it can be seen that the distance between each layer of gold atoms is given by $x$. Thus, remembering that the gold lattice is flanked by a layer of gold atoms at both ends, the thickness is given by:
$\textrm{Thickness} = (n-1) \times x\;.$
Using the most sophisticated value of n gives:
$\textrm{Thickness} = (65380 - 1) \times \sqrt{2} r_{gold\ atom}= 65379 \times \sqrt{2} \times 135 \times 10^{-12} = \mathbf{12.5 \mu m}\;.$