• Warm-up
• Try this next
• Think higher
• Read: mathematics
• Read: science
• Explore further

This problem makes use of vectors, coordinates and scalar products. It is a very useful fact that if two vectors ${\bf u}$ and ${\bf v}$ have coordinates $(x_1, y_1, z_1)$ and $(x_2, y_2, z_2)$ then the cosine of the angle $\theta$ they make is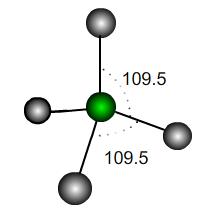
$$
\cos(\theta) = \frac{{\bf u}\cdot {\bf v}}{|{\bf u}||{\bf v}|}\quad\,,\mbox{ where } {\bf u}\cdot {\bf v}=x_1x_2+y_1y_2+z_1z_2
$$
This is useful, because if we can label the coordinates of the atoms in a molecule or crystal then we can easily work out the angles between the bonds.

 

In a perfect tetrahedral molecule there is a central atom attached to four other atoms which lie on the vertices of a perfect tetrahedron. If the central atom is at the coordinate origin and the molecule rests on the plane $z=-h$ then what would be the coordinates of the other atoms, assuming a bond length of $1$ unit? Find the scalar products between the vectors joining the origin to each atom and hence the value of $h$. It is usually stated that the angles each of these bonds make is $109.5^\circ$; however, this is only an approximation. What is the exact value of the bond angle in a perfect tetrahedron? If the perfect tetrahedron is deformed slightly, how many of the bond angles could be exactly $109.5^\circ$? How would it be deformed to achieve this? Would the other bond angles increase or decrease under such a deformation?

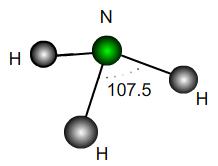
A perfect trigonal pyramidal molecule is the same as a perfect tetrahedral molecule with a single outer atom removed. Ammonia NH$_3$ is approximately a trigonal pyramid with bond angle $107.5$. Does this correspond to a lengthening or shortening of the bonds relative to a perfect structure? By what percentage? If the H atoms were fixed and a vertical force were applied downwards to the N atom in the diagram, would the bond angles increase or decrease? What would be the maximum possible angle mathematically?