Factors and Multiples Puzzle
Using your knowledge of the properties of numbers, can you fill all the squares on the board?
Problem
To try this puzzle you will need a copy of the playing board and cards. You can download a copy to print.
Cut out the $10$ heading cards and put one in each of the $10$ spaces round the playing board.
Image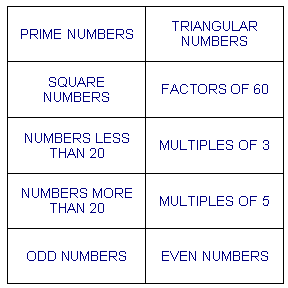
Cut out the $25$ number cards and place each one in a different square on the playing board so that the number satisfies the condition given by the heading card for that row and the condition given by the heading card for that column.
Image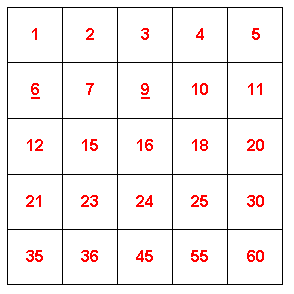
By rearranging the heading cards and the number cards, try to fill as many squares on the playing board as possible.
Can you fill all the squares on the board at once?
Getting Started
Can a number be both odd and even?
What does this tell you about where the ODD NUMBER and EVEN NUMBER headings have to go?
Can you use this idea to position any of the other heading cards?
If you have reached a stage where you have placed most of the numbers but have a few that you cannot place, don't panic!
Could you swap one of the numbers that you can't place for a number that is already on the grid?
You might be able to swap them and then find that the number you have removed can be placed on one of the empty squares.
Don't forget: $1$ is not a prime number!
Triangle numbers can be represented by a triangular array of squares
Student Solutions
Xavier Irymple Secondary College in Australia started with square and triangluar numbers. Here is Xavier's work and completed grid:
I decided to work with square numbers on the opposite side of triangular numbers, since the number 1 was relevant to both of them. Then I placed both the triangular numbers and square numbers in their relevant place. Then I just built the rest around those numbers and categories.

Andrea from Norwich School in the UK noticed that some of the categories could not share any numbers. Here is Andrea's method and completed grid, which is different to Xavier's:
I started out by doing trial and error, but soon realised that headings like NUMBERS LESS THAN TWENTY and NUMBERS MORE THAN TWENTY needed to be on the same row. TRIANGULAR NUMBERS and SQUARE NUMBERS both had the number 36, so I had to put them with an intersecting square. I then just filled in the rest of the squares.

Sehar, Saanvi, Dhanvin, Aariz,Vivaan, Sai, Paavani, Utkarsh, Tavish and Dhruv from Ganit Kreeda, Emily, Mason and Summer, Tyler and Frankie and Jakob from Irymple Secondary College, James and Aarush from Norwich School and Dean from Saint Spyridon College in Australia also found categories with little or no overlap. They didn't all choose the same categories, and all found different grids. Here is Dean's approach, and by clicking below you can see each of the grids.
Dean started this challenge by thinking about the heading cards and where they could be placed based on his knowledge of number properties.
He realised that the 'numbers less than 20' and 'numbers more than 20' needed to be placed on the same side of the gameboard to avoid a clash.
From here, Dean then realised that this mathematical thinking would help him to place the other heading cards around the game board correctly. He
noticed that 'even numbers' and 'odd numbers' also needed to be placed on the same side of the board. Similarly, 'triangular numbers' and 'square numbers' did not have many possible answers on the number cards provided, so Dean realised that it would be best to work with these heading cards and the relevant numbers before attempting the others. In this way, he knew that the remaining number cards were more versatile and that he could place them in different places because they shared common number properties. With strong perseverance, Dean was able to successfully complete the puzzle independently.
Click to see the grids filled in using similar methods:







Jackson and Declan from Irymple Secondary College and Pranathi and Ananthjith from Ganit Kreeda used systematic listing methods. Here is some of James and Declan's method, and their completed grid (which is different to all the grids we've seen before):
Solving the Factors and Multiples Puzzles was both challenging and rewarding. [We] approached it methodically, starting with a clear understanding of the concepts. First, [we] checked to see what 5 headings fit all 25 numbers then put the 5 headings on one row but if all the numbers didn’t fit with the row and the column [we] would try the strategy again.

These are the Pranathi's lists and grid. Note that, although Pranathi has not ticked 1 as a prime number, it is included as a prime number on Pranathi's grid, which isn't quite right.



Ananthajith's work shows how Ananthajith used listing to create a final grid (which, again, is different to all the grids above):


Isaac and Alexandre used a similar systematic listing method, and found all possible number combinations for a certain arangement of the categories into rows and columns. They used the programming language Python. Click here to open their work.
We received some more complete grids with no methods. These grids are all different to any of the grids above. Click to see the complete grids.



Teachers' Resources
Why do this problem?
This puzzle provides an interesting context which challenges students to apply their knowledge of the properties of numbers. Students need to work with various types of numbers at the same time and consider their relationships to each other (e.g. primes, squares and specific sets of multiples). This is an ideal follow up to Number Families.
Possible approach
This printable worksheet may be useful: The Factors and Multiples Puzzle
Show a $3 \times 3$ grid with six headings on the board, ask students to suggest numbers that could fit into each of the nine segments (an easy start, but useful revision of vocabulary).
The students (ideally working in twos or threes) can then be set the challenge of filling the $5 \times 5$ board with the available numbers. The challenge is to fit all 25 number cards onto the grid, so if they haven't been able to find a 'home' for all the number cards, suggest that they move some of the property cards around.
There is more than one possible solution so students could display their different arrangements. When a student/pair finishes allocating numbers to a grid, they should record the grid headings and how many numbers they placed.
A concluding plenary could ask students to share any insights and strategies that helped them succeed at this task.
A teacher comments:
Key questions
Which numbers are hard to place?
Encourage students to pay attention to the order in which they allocate numbers to cells - recognising the key cells to fill, and the key numbers to place.
Possible support
Some students could be given a larger range of numbers to choose from, or offered a smaller grid and appropriately restricted numbers - this could work with students choosing from the full set of $10$ categories, or with an adapted set.
Possible extension
Teachers can adapt the task by changing the heading cards or by asking students to create a new set of heading cards and a set of numbers that make it possible to fill the board. Students could then swap their new puzzles.
Is it possible to create a puzzle that can be filled with $25$ consecutive numbers?
Handouts for teachers are available here (word document, pdf document), with the problem on one side and the notes on the other.
