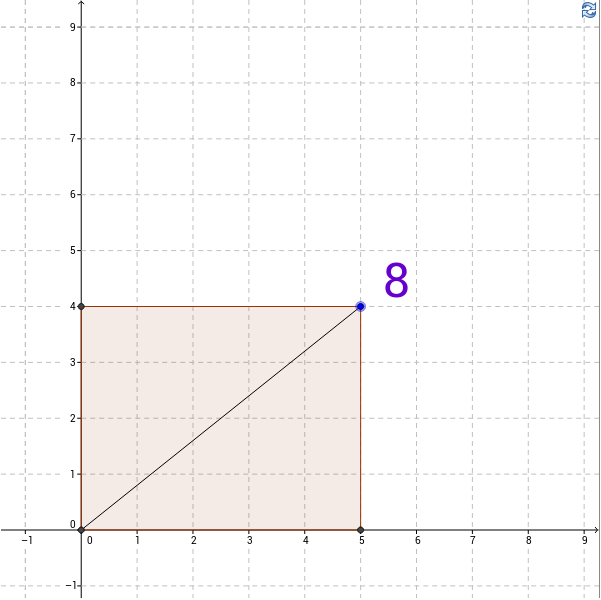
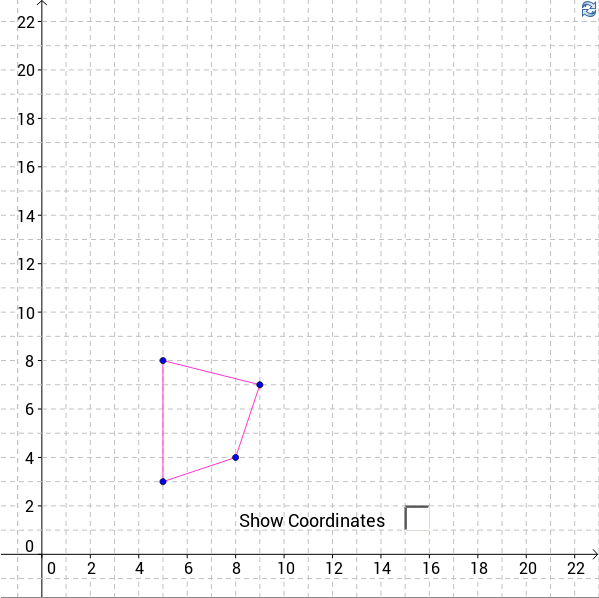
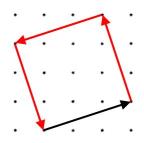
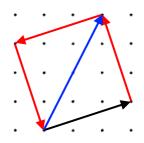
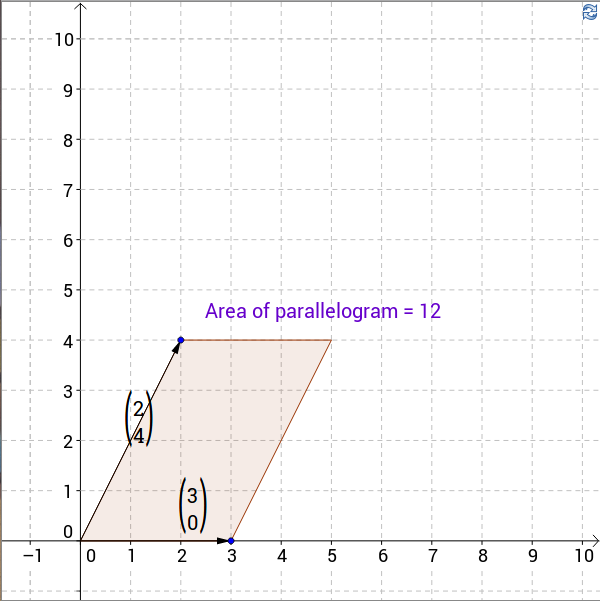
Take some time to look at the route followed by the arrows in this diagram. Can you now look away and list the points visited?
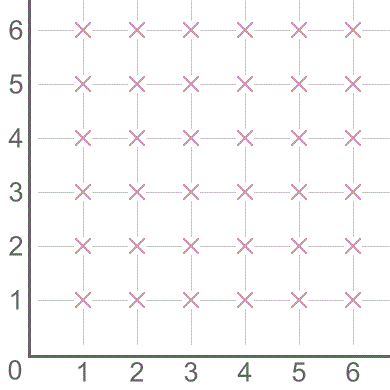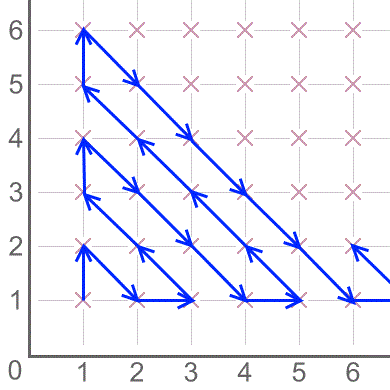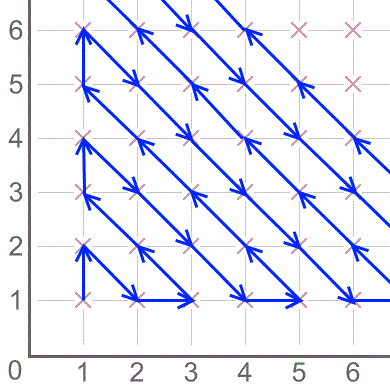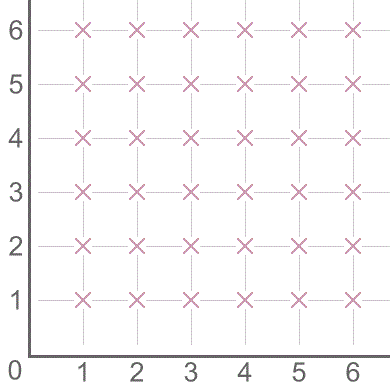
If the pattern of arrows continues for ever, which point will be the 100th to be visited?
How many steps will it take to reach (60,40)?
Where will the next step take you to?
Can you design an alternative route that visits all the points on a grid?
Can you still work out how many steps it will take you to reach (60,40)?