Exploring distances
Getting Round the City

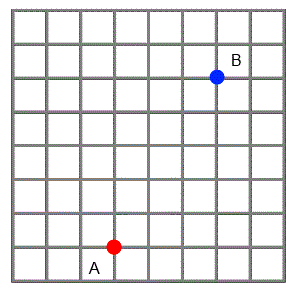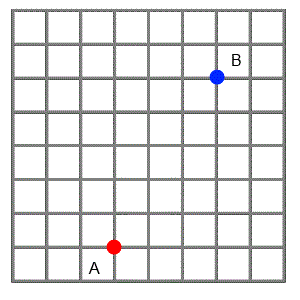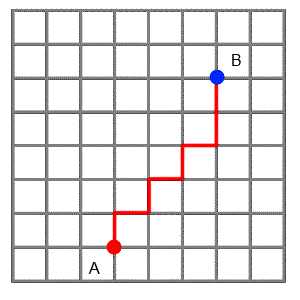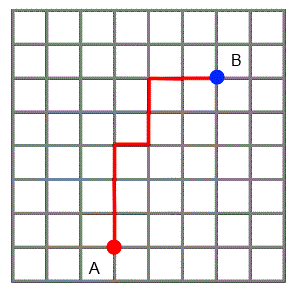
The grid below represents a city laid out in "blocks" with all the roads running north-south, or east-west.

Imagine two friends live where the red and blue dots are on the grid.

The animation shows three paths that one friend could choose if he wanted to visit the other.

He likes to find the shortest routes possible, so he always travels north or east, never south or west.

What interesting mathematical questions could you explore on a city grid like this one?

Some other ideas

The grid below represents a city laid out in "blocks" with all the roads running north-south, or east-west.

Imagine two friends live where the red and blue dots are on the grid.

The animation shows three paths that one friend could choose if he wanted to visit the other.

He likes to find the shortest routes possible, so he always travels north or east, never south or west.

Tools
Find the Robber

Can you help the police locate the robber?

The robber is hiding at a crossroads in a modern city, where the roads are all at right angles and equally spaced.

Choose coordinates where you think the robber might be hiding. The interactivity tells you the shortest distance to the robber, travelling along the roads.

Try to find the robber using only a few guesses.

To use our interactivity, click on the thumbnail!

Can you guarantee to always find the robber in less than five guesses? Can you do better than this?

How would your strategy change if the robber were allowed to move 1 block after each guess?

Can you think of any other mathematically interesting variations of the game?

Tools
Find the Metagiff

In a three dimensional city on a distant planet, the metagiff has escaped from the zoo! Can you help the sheriff locate the metagiff?

The metagiff is hiding at a point on the three dimensional grid, so his location is specified by three coordinates (x,y,z).

Choose coordinates where you think the metagiff might be hiding. The interactivity tells you the shortest distance to the metagiff, travelling along the grid lines.

Try to find the metagiff using only a few guesses.

To use our interactivity, click on the thumbnail!

Can you guarantee to always find the metagiff in less than six guesses? Can you do better than this?

How would your strategy change if the metagiff were allowed to move 1 space after each guess??

Can you think of any other mathematically interesting variations of the game?

Tools