Cubes and cuboids

problem
Icosian game

Age

11 to 14

Challenge level

This problem is about investigating whether it is possible to start at one vertex of a platonic solid and visit every other vertex once only returning to the vertex you started at.
problem
Marbles in a box

Age

11 to 16

Challenge level

How many winning lines can you make in a three-dimensional version of noughts and crosses?
problem
Counting triangles

Age

11 to 14

Challenge level

Triangles are formed by joining the vertices of a skeletal cube. How many different types of triangle are there? How many triangles altogether?
problem
Take ten

Age

11 to 14

Challenge level

Is it possible to remove ten unit cubes from a 3 by 3 by 3 cube so that the surface area of the remaining solid is the same as the surface area of the original?
problem
Nine colours

Age

11 to 16

Challenge level

Can you use small coloured cubes to make a 3 by 3 by 3 cube so that each face of the bigger cube contains one of each colour?
problem
Plutarch's boxes

Age

11 to 14

Challenge level

According to Plutarch, the Greeks found all the rectangles with integer sides, whose areas are equal to their perimeters. Can you find them? What rectangular boxes, with integer sides, have their surface areas equal to their volumes?
problem
How many dice?

Age

11 to 14

Challenge level

A standard die has the numbers 1, 2 and 3 are opposite 6, 5 and 4 respectively so that opposite faces add to 7? If you make standard dice by writing 1, 2, 3, 4, 5, 6 on blank cubes you will find there are 2 and only 2 different standard dice. Can you prove this ?
problem
Boxed in

Age

11 to 14

Challenge level

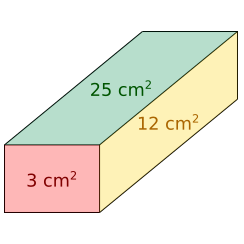
A box has faces with areas 3, 12 and 25 square centimetres. What is the volume of the box?
problem
Tic tac toe

Age

11 to 14

Challenge level

In the game of Noughts and Crosses there are 8 distinct winning lines. How many distinct winning lines are there in a game played on a 3 by 3 by 3 board, with 27 cells?
problem
Painting cubes

Age

11 to 14

Challenge level

Imagine you have six different colours of paint. You paint a cube using a different colour for each of the six faces. How many different cubes can be painted using the same set of six colours?