Conjecturing and generalising

problem
Favourite

Vector Journeys

Age

14 to 18

Challenge level

Charlie likes to go for walks around a square park, while Alison likes to cut across diagonally. Can you find relationships between the vectors they walk along?
problem
Favourite

Which Spinners?

Age

14 to 18

Challenge level

Can you work out which spinners were used to generate the frequency charts?
problem
Favourite

Summing Geometric Progressions

Age

14 to 18

Challenge level

Watch the video to see how to sum the sequence. Can you adapt the method to sum other sequences?
problem
Favourite

Negative Powers

Age

14 to 18

Challenge level

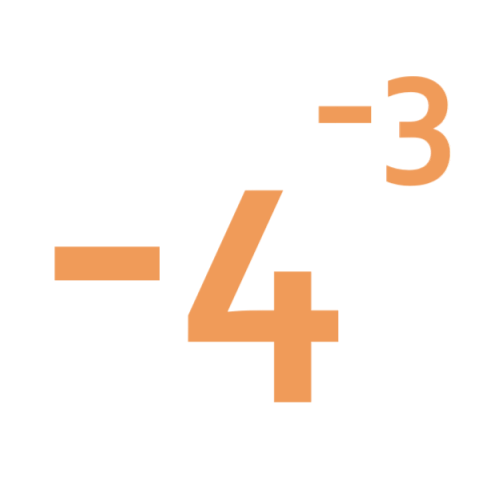
What does this number mean? Which order of 1, 2, 3 and 4 makes the highest value? Which makes the lowest?
problem

All Tangled Up

Age

14 to 18

Challenge level

Can you tangle yourself up and reach any fraction?
problem

Difference of Odd Squares

Age

14 to 18

Challenge level

$40$ can be written as $7^2 - 3^2.$ Which other numbers can be written as the difference of squares of odd numbers?
problem

Degree Ceremony

Age

16 to 18

Challenge level

Can you find the sum of the squared sine values?
problem

Chord

Age

16 to 18

Challenge level

Equal touching circles have centres on a line. From a point of this line on a circle, a tangent is drawn to the farthest circle. Find the lengths of chords where the line cuts the other circles.
problem

Least of All

Age

16 to 18

Challenge level

A point moves on a line segment. A function depends on the position of the point. Where do you expect the point to be for a minimum of this function to occur.
problem
Favourite

Tangled Trig Graphs

Age

16 to 18

Challenge level

Can you work out the equations of the trig graphs I used to make my pattern?