The Wheatstone bridge
Problem
The circuit below is known as a Wheatstone bridge, a device popularized by Sir Charles Wheatstone. The purpose of the Wheatstone bridge is to measure some unknown impedance. This is achieved by 'balancing' the two legs of bridge, one will contain a variable resistor and the other the component whose impedance we wish to measure.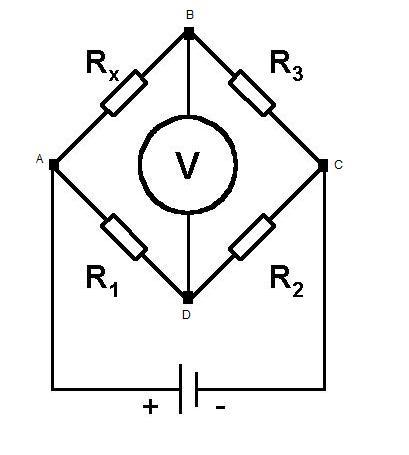
Can you find the condition on the variable resistor needed for balance ($V = 0$) using loop current analysis?
Can you find the condition for balance using a potential divider argument?
Extension:
If we now replace the DC voltage source with an AC voltage source of frequency $f$, add a capacitor $C_3$ in series with $R_3$ and added a second capacitor $C_2$ in parallel with $R_2$, at what frequency will balance occur, in terms of $R_1,R_2,C_2,R_3,C_3$ and $R_x$?
Student Solutions
We can solve the problem using a potential divider or using loop currents.
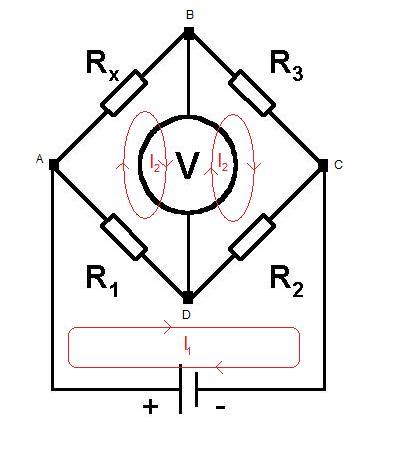
Loop Currents:
We can assign loop currents to each loop as shown above. At balance the vector sum of the currents through the meter will be zero, we can therefore assign $I_2$to both the left and right loop, the currents will cancel through the meter.
Applying Kirchoff's voltage law to each loop we find that:
$\sum_{Voltages} Left Hand Loop = - (I_2 - I_1)R_1 - I_2 R_x = 0 $
$\sum_{Voltages}Right Hand Loop = -I_2 R_3 -(I_2 - I_1)R_2 = 0 $
We have two independent equations and two unknowns ($I_1$ and $I_2$).
From the left loop: $I_2 = \frac{R_1}{R_1 + R_x} I_1$
From the right loop: $I_2 = \frac{R_2}{R_3 + R_2} I_1$
Equating we see:
$R_1R_3 = R_2R_x$
Potential Divider:
At balance $V_b = V_d$
The potential at C is zero (ground). The potential at A is therefore divided between $R_x$ and $R_3$, in addition it is also divided between $R_1$and $R_2$ .
By potential divider:
$V_b = \frac{R_3}{R_x} V_a$
$V_d = \frac{R_2}{R_1}V_a$
Equating $V_b$ and $V_d$
$R_1 R_3 = R_2 R_x$
Extension:
If we replace:
$R_2 = Z_2$
We find $Z_2$ by combing the impedance of $C_2$ in parallel with $R_2$
$Z_2= \frac{R_2 \frac{1}{2 \pi f t C \bf i}} {R_2 + 2 \pi f t C \bf i }$
where $i = \sqrt{-1} = i$
$R_3 = Z_3 = $
We find $Z_3$ by combining the imperdance of $C_3$ in series with $R_3$
where $i = \sqrt{-1} = i$
From part 1 we know that:
$R_1Z_3 = Z_2R_x$
Substituting $Z_3$, $Z_4$ and equating real and imaginary terms we find that:
the real part tells us nothing about frequency (cancels)
The imaginary part tells us f = $\frac{1}{2 \pi} \sqrt{\frac{1}{C_3 C_2 R_3 R_2}} $ at balance
