Bond angles
Think about the bond angles occurring in a simple tetrahedral
molecule and ammonia.
Problem
This problem makes use of vectors, coordinates and scalar products. It is a very useful fact that if two vectors ${\bf u}$ and ${\bf v}$ have coordinates $(x_1, y_1, z_1)$ and $(x_2, y_2, z_2)$ then the cosine of the angle $\theta$ they make is
Image
$$
\cos(\theta) = \frac{{\bf u}\cdot {\bf v}}{|{\bf u}||{\bf v}|}\quad\,,\mbox{ where } {\bf u}\cdot {\bf v}=x_1x_2+y_1y_2+z_1z_2
$$
This is useful, because if we can label the coordinates of the atoms in a molecule or crystal then we can easily work out the angles between the bonds.
|
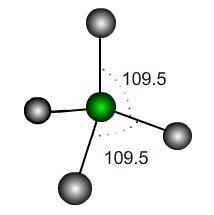
In a perfect tetrahedral molecule there is a central atom attached to four other atoms which lie on the vertices of a perfect tetrahedron.
If the central atom is at the coordinate origin and the molecule rests on the plane $z=-h$ then what would be the coordinates of the other atoms, assuming a bond length of $1$ unit? Find the scalar products between the vectors joining the origin to each atom and hence the value of $h$.
It is usually stated that the angles each of these bonds make is $109.5^\circ$; however, this is only an approximation. What is the exact value of the bond angle in a perfect tetrahedron?
If the perfect tetrahedron is deformed slightly, how many of the bond angles could be exactly $109.5^\circ$? How would it be deformed to achieve this? Would the other bond angles increase or decrease under such a deformation?
|
Image

|
|
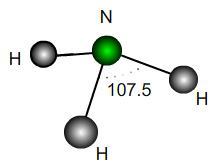
A perfect trigonal pyramidal molecule is the same as a perfect tetrahedral molecule with a single outer atom removed. Ammonia NH$_3$ is approximately a trigonal pyramid with bond angle $107.5$. Does this correspond to a lengthening or shortening of the bonds relative to a perfect structure? By what percentage?
If the H atoms were fixed and a vertical force were applied downwards to the N atom in the diagram, would the bond angles increase or decrease? What would be the maximum possible angle mathematically?
|
Image
|
Getting Started
Try drawing the tetrahedral molecule with some axes on it and use
simple trigonometry to define the coordinates of each of the outer
atoms. It may be useful to let one of the bottom atoms to lie along
an axis. To find the coordinates of the other two bottom atoms, it
is easiest to draw a top-down diagram to help...
Student Solutions
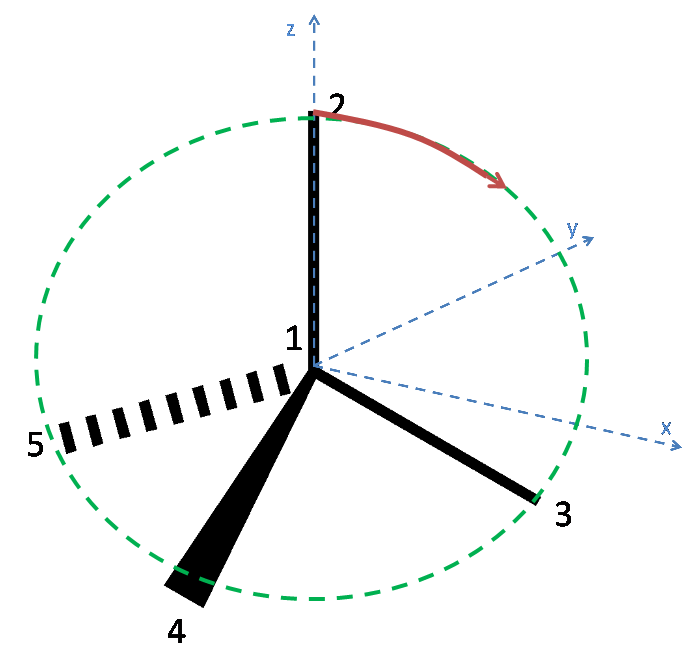
Below is a diagram of the tetrahedral molecule, along with axes and labelled atoms:
Image
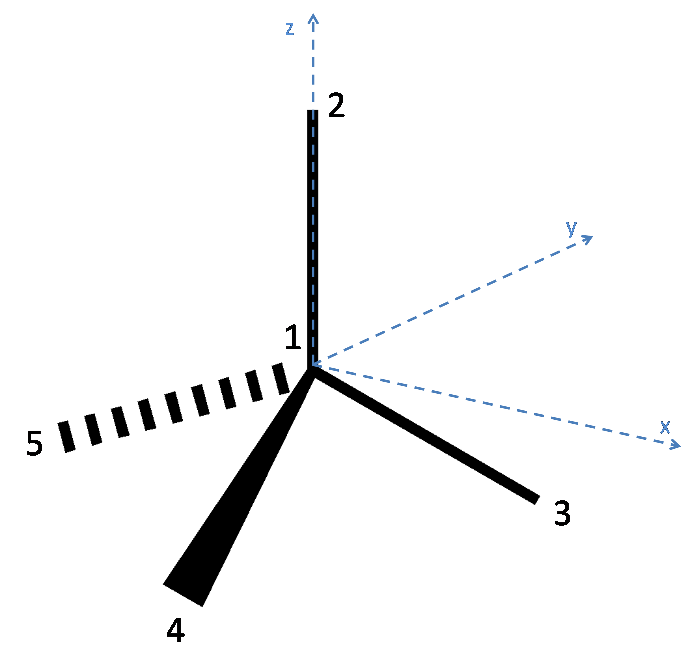
As has been stated in the question, Atom 1 has coordinates (0,0,0). Additionally, since the atoms 3, 4 and 5 lie on the plane $z = -h$, it can be reasoned that Atom 2 lies on the z axis and so has coordinates (0, 0, 1).
To define the coordinates of atoms 3, 4 and 5, the x and y axes must be placed arbitrarily. To make the algebra simpler, the x axis is placed such that atom 3 lies along it. Thus the coordinates of Atom 3 are (x,0,-h) where x is a quantity to be determined. Since each bond is of unit length, x can be found as follows:
$\sqrt{x^2 + h^2} = 1$
$\therefore x = \sqrt{1 - h^2}$
Thus Atom 3 has coordinates ($\mathbf{\sqrt{1 - h^2}}$,0,-h).
To find the coordinates of atoms 4 and 5, it is easier to view the tetrahedron by looking down the z-axis:
Image

From here, it can be seen that the three bonds are equally spaced and so must be separated by an angle of 120$^\circ$ in the plane. It has already been shown that the length of each of these bonds is $x$ in the plane, and so the length along the x and y axes for Atoms 4 and 5 can be easily calculated using trigonometry:
Atom 5 has $x\cos(30)$ along the y axis, and $-x\sin(30)$ along the x axis.
Atom 4 has $-x\cos(30)$ along the y axis and $-x\sin(30)$ along the x axis.
As the atoms 3, 4 and 5 lie in the plane z = -h, the coordinates for atoms 4 and 5 are as follows:
Atom 4: ( $-x\sin(30)$, $-x\cos(30)$, -h) = ($\mathbf{-\sqrt{1 - h^2}\sin(30), -\sqrt{1-h^2}\cos(30), -h}$)
Atom 5: ( $-x\sin(30)$, $x\cos(30)$, -h) = ($\mathbf{-\sqrt{1 - h^2}\sin(30), \sqrt{1-h^2}\cos(30), -h}$)
The coordinates of the atoms 2, 3, 4, and 5 have now been found. Their position vectors from Atom 1 are the same as their coordinates, since Atom 1 is at the origin. Using scalar products between pairs of position vectors, with the knowledge that their angular separation (i.e. bond angle) should be the same, yields values for h and also for the bond angle:
Dotting 2 and 3: $ -h = \cos(\theta)$
Dotting 3 and 4: $ \frac{3}{2}h^2 + \frac{1}{2} = \cos(\theta)$
Combinging these equations to eliminate $\cos(\theta)$ gives:
$3h^2 + 2h -1 =0$
$ h = -1\ \text{or}\ h = \frac{1}{3}$
A positive value for h is clearly needed:
$\mathbf{h = \frac{1}{3}}$
$\therefore \mathbf{cos(\theta)} = -\frac{1}{3}$
$\rightarrow \mathbf{Bond\ angle = arccos(\frac{-1}{3})}$
There are many different ways to deform the perfect tetrahedron, which lead to a variety of different numbers of bond angles being preserved. It is possible to deform the tetrahedron in such a way that 4 bond angles remain at 109.5$^\circ$ and one bond angle is increased, and another concomitantly decreased.
Look at the tetrahedron illustrated below. Atom 2 can be moved towards Atom 3, which will leave the following angles preserved: Atom 4 to 5, Atom 4 to 3, Atom 3 to 5, and Atom 4 to 2. The last of these angles is only preserved if the bond length of Atom 4 remains fixed, such that Atom 4 moves towards atom two along the arc of a circle. It can clearly be seen also that the angle between Atom 2 and 3 decreases, and that the angle between 2 and 5 increases!
Image
The second part of this problem involves the trigonal pyramidal ammonia molecule. We have effectively moved an atom from the tetrahedron, and squashed the three remaining atoms closer together. It can be clearly visualised that the bond lengths must be increased in order to maintain the same distance between the hydrogens.To calculate what percent we must first calculate the distance between the hydrogens in the tetrahedron:
Image
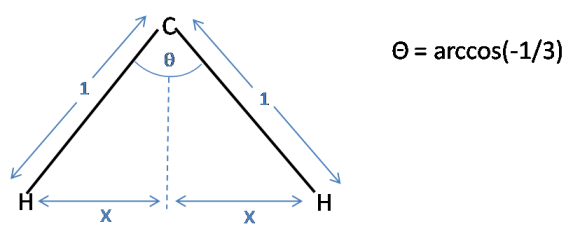
Using simple trigonometry $x$ can be calculated:
$\sin(\frac{\theta}{2}) = \frac{x}{1}$
$x = \sin(\frac{1}{2}\arccos(-\frac{1}{3}))$
Now consider a triangle for the ammonia molecule. Note that the distance between the hydrogens is $2x$, as in the tetrahedron:
Image
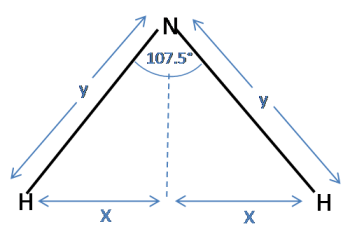
Again, using trigonometry:
$\sin(\frac{107.5}{2}) = \frac{x}{y}$
Substituting for $x$ and rearranging to find $y$ gives:
$ y = \frac{\sin(\frac{1}{2}\arccos(-\frac{1}{3}))}{\sin(\frac{107.5}{2})} = 1.0125$
Therefore, the percentage increase is 1.25%.
If the hydrogen atoms remained fixed and a vertical force was applied to the N atom, the maximum bond angle would be seen when the molecule became planar. In these circumstances, the three hydrogen atoms would be in the same plane as the nitrogen atom, and would be distributed around it at 120$^\circ$ intervals. Thus, the maximum theoretical bond angle for the trigonal pyramidal arrangement is $\mathbf{120^\circ}$.
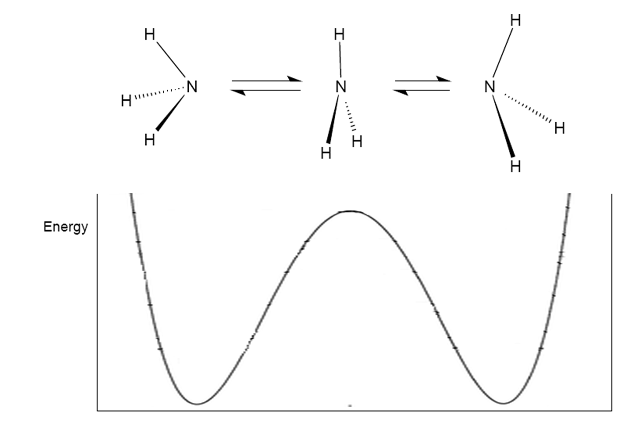
Although it can be seen that the formation of the planar ammonia molecule requires much energy, this is an observed phonomenon. At room temperature, ammonia rapidly inverts (~ 10$^{12}$ times per second), much like an umbrella turning inside out in the wind. In order to invert, the molecule must pass through a high-energy unstable planar transition state:
Image