Number Sense Series: Developing Early Number Sense
You can read an updated version of this article in our Number Sense and Place Value Feature.
What is number sense?
The term "number sense" is a relatively new one in mathematics education. It is difficult to define precisely, but broadly speaking, it refers to "a well organised conceptual framework of number information that enables a person to understand numbers and number relationships and to solve mathematical problems that are not bound by traditional algorithms" (Bobis, 1996). The National Council of
Teachers (USA, 1989) identified five components that characterise number sense: number meaning, number relationships, number magnitude, operations involving numbers and referents for numbers and quantities. These skills are considered important because they contribute to general intuitions about numbers and lay the foundation for more advanced skills.
Researchers have linked good number sense with skills observed in students proficient in the following mathematical activities:
- mental calculation (Hope & Sherrill, 1987; Trafton, 1992);
- computational estimation (for example; Bobis, 1991; Case & Sowder, 1990);
- judging the relative magnitude of numbers (Sowder, 1988);
- recognising part-whole relationships and place value concepts (Fischer, 1990; Ross, 1989) and;
- problem solving (Cobb et.al., 1991).
How does number sense begin?
Usually, when presented with more than five objects, other mental strategies must be utilised. For example, we might see a group of six objects as two groups of three. Each group of three is instantly recognised, then very quickly (virtually unconsciously) combined to make six. In this strategy no actual counting of objects is involved, but rather a part-part-whole relationship and rapid mental addition is used. That is, there is an understanding that a number (in this case six) can be composed of smaller parts, together with the knowledge that 'three plus three makes six'. This type of mathematical thinking has already begun by the time children begin school and should be nurtured because it lays the foundation for understanding operations and in developing valuable mental calculation strategies.
What teaching strategies promote early number sense?
Learning to count with understanding is a crucial number skill, but other skills, such as perceiving subgroups, need to develop alongside counting to provide a firm foundation for number sense. By simply presenting objects (such as stamps on a flashcard) in various arrangements, different mental strategies can be prompted. For example, showing six stamps in a cluster of four and a pair prompts
the combination of 'four and two makes six'. If the four is not subitised, it may be seen as 'two and two and two makes six'. This arrangement is obviously a little more complex than two groups of three. So different arrangements will prompt different strategies, and these strategies will vary from person to person.
If mental strategies such as these are to be encouraged (and just counting discouraged) then an element of speed is necessary. Seeing the objects for only a few seconds challenges the mind to find strategies other than counting. It is also important to have children reflect on and share their strategies (Presmeg, 1986; Mason, 1992). This is helpful in three ways:
- verbalising a strategy brings the strategy to a conscious level and allows the person to learn about their own thinking;
- it provides other children with the opportunity to pick up new strategies;
- the teacher can assess the type of thinking being used and adjust the type of arrangement, level of difficulty or speed of presentation accordingly.
To begin with, early number activities are best done with moveable objects such as counters, blocks and small toys. Most children will need the concrete experience of physically manipulating groups of objects into sub-groups and combining small groups to make a larger group. After these essential experiences more static materials such as 'dot cards' become very useful.
Dot cards are simply cards with dot stickers of a single colour stuck on one side. (However, any markings can be used. Self-inking stamps are fast when making a lot of cards). The important factors in the design of the cards are the number of dots and the arrangement of these dots. The various combinations of these factors determine the mathematical structure of each card, and hence the types of
number relations and mental strategies prompted by them.
Consider each of the following arrangements of dots before reading further. What mental strategies are likely to be prompted by each card? What order would you place them in according to level of difficulty?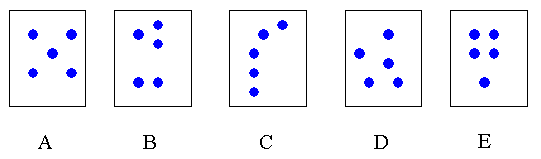
Card A is the classic symmetrical dice and playing card arrangement of five and so is often instantly recognised without engaging other mental strategies. It is perhaps the easiest arrangement of five to deal with.
Card B presents clear sub-groups of two and three, each of which can be instantly recognised. With practice, the number fact of 'two and three makes five' can be recalled almost instantly.
Card C: A linear arrangement is the one most likely to prompt counting. However, many people will mentally separate the dots into groups of two and three, as in the previous card. Other strategies such as seeing two then counting '3, 4, 5' might also be used.
Card D could be called a random arrangement, though in reality it has been quite deliberately organised to prompt the mental activity of sub-grouping. There are a variety of ways to form the sub-groups, with no prompt in any particular direction, so this card could be considered to be the most difficult one in the set.
Card E shows another sub-group arrangement that encourages the use (or discovery) of the 'four and one makes five' number relation.
Obviously, using fewer than five dots would develop the most basic number sense skills, and using more than five dots would provide opportunities for more advanced strategies. However, it is probably not useful to use more than ten dots. (See the follow-on article focusing on developing a 'sense of ten' and 'place value readiness'). Cards such as these can be shown briefly to
children, then the children asked how many dots they saw. The children should be asked to explain how they perceived the arrangement, and hence what strategies they employed.
What games can assist development of early number sense?
Games can be very useful for reinforcing and developing ideas and procedures previously introduced to children. Although a suggested age group is given for each of the following games, it is the children's level of experience that should determine the suitability of the game. Several demonstration games should be played, until the children become comfortable with the rules and procedures of
the games.
Deal and Copy (4-5 years) 3-4 players
Materials: 15 dot cards with a variety of dot patterns representing the numbers from one to five and a plentiful supply of counters or buttons.
Rules: One child deals out one card face up to each other player. Each child then uses the counters to replicate the arrangement of dots on his/her card and says the number aloud. The dealer checks each result, then deals out a new card to each player, placing it on top of the previous card. The children then rearrange their counters to match the new card.
This continues until all the cards have been used.
Variations/Extensions
- Each child can predict aloud whether the new card has more, less or the same number of dots as the previous card. The prediction is checked by the dealer, by observing whether counters need to be taken away or added.
- Increase the number of dots on the cards.
- Increase the number of pairs of cards used.
- Use a greater number of dots on the cards.
- Pair a dot card with a numeral card.
- Try to turn the spread cards that give the minimum difference, so the winner is the player with the fewest counters.
- Roll a die instead of using pile cards. Start with a set number of counters (say 20), so that when all the counters have been claimed the game ends.
- Use dot cards with random arrangements of dots.
The next article in this series is entitled A Sense of 'ten' and Place Value.
