Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Matter of Scale
Age 14 to 16
Challenge Level 





Take any right-angled triangle with side lengths $a, b$ and $c$. For convenience, label the two acute angles $x^{\circ}$ and $y^{\circ}$.

Make two enlargements of the triangle, one by scale factor $a$ and and one by scale factor $b$:
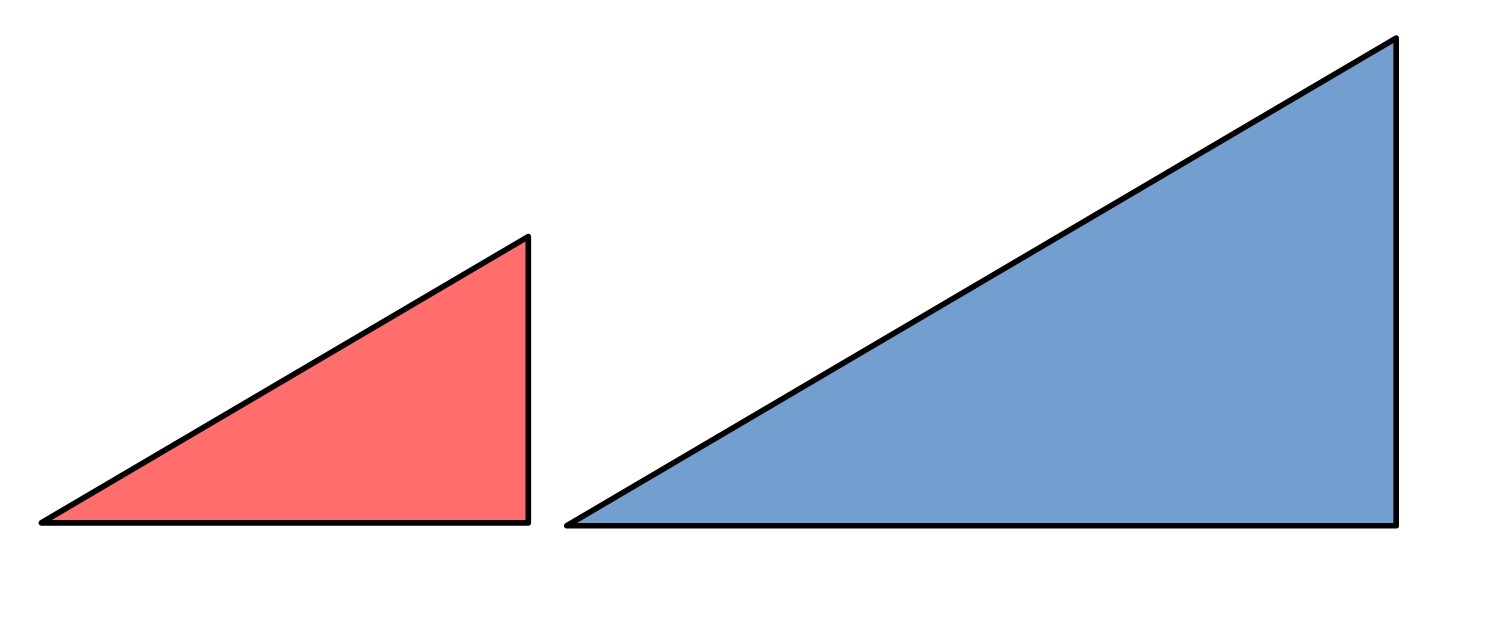
What are the lengths of these new triangles?
Draw out a copy of them and indicate what the lengths and the angles are in each.
Draw out a copy of them and indicate what the lengths and the angles are in each.
We can put these two triangles together to make a larger triangle.
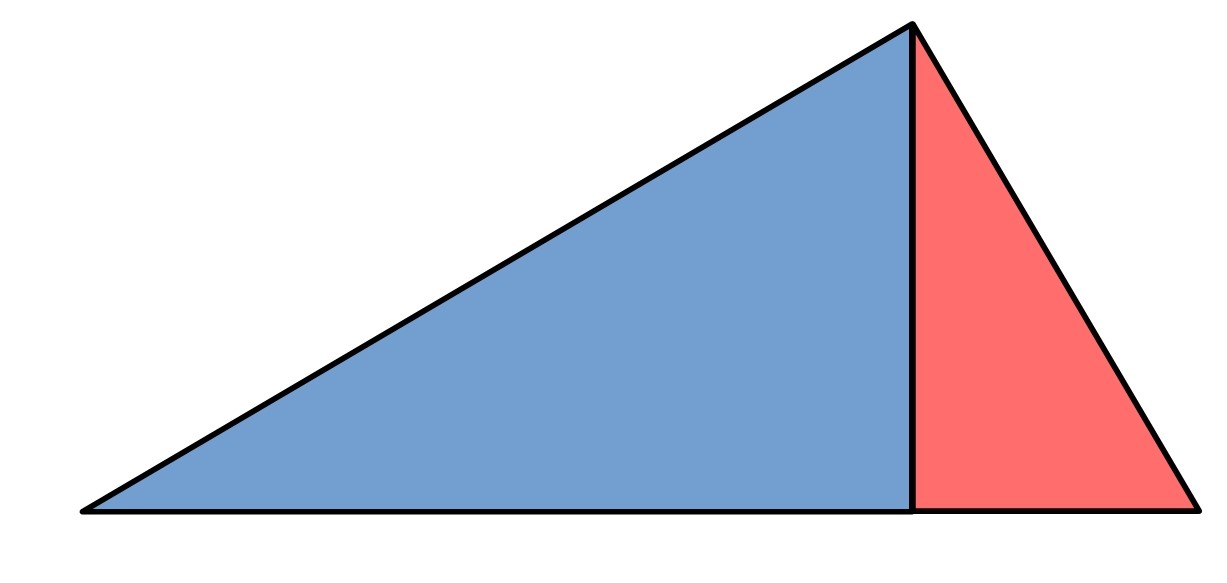
Find the lengths and angles in this last triangle.
Can you show that this triangle is similar to the original triangle?
What is the scale factor of enlargement between the first and last triangles?
Can you use your results to prove Pythagoras' Theorem?
You might like to explore some more proofs of Pythagoras' Theorem, and a proof of The Converse of Pythagoras' Theorem.
We are very grateful to the Heilbronn Institute for Mathematical Research for their generous support for the development of this resource.