 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Matter of Scale



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Well done to Nayanika from The Tiffin Girls' School, Yihuan form Pate's Grammar School, John from Calthorpe Park School in the UK and Andrew from Island School, who all sent in correct proofs.
This is John's work:
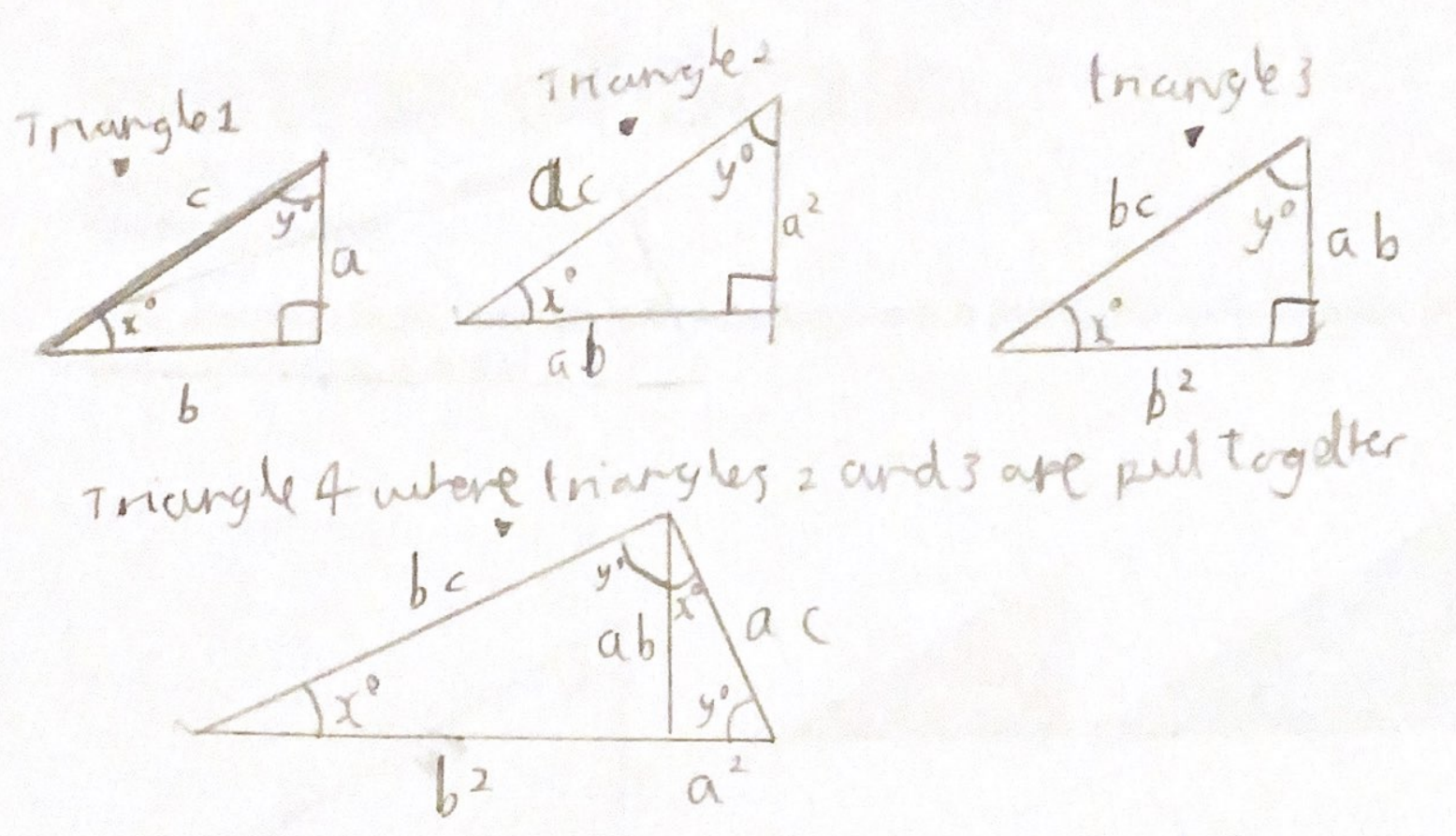
The four triangles are similar by AA similarity (they all share two angles - and therefore all 3 angles). As triangle 4 is similar to triangle 1 its corresponding parts are in equal ratios.
$\therefore a:ac$ is the same ratio as $c:a^2+b^2$
$\therefore 1:c$ $=$ $c:a^2+b^2$
$\therefore 1:c$ $=$ $1:\dfrac{a^2+b^2}{c}$
$\therefore c = \dfrac{a^2+b^2}{c}$
Which is rearranged to $a^2+b^2=c^2$
Alternatively we can think of triangle 4 as triangle 1 enlarged by a scale factor of $c$.
Therefore $a^2+b^2 = c\times c$
So $a^2+b^2=c^2$
You may also like
Some(?) of the Parts
A circle touches the lines OA, OB and AB where OA and OB are perpendicular. Show that the diameter of the circle is equal to the perimeter of the triangle
Ladder and Cube
A 1 metre cube has one face on the ground and one face against a wall. A 4 metre ladder leans against the wall and just touches the cube. How high is the top of the ladder above the ground?
At a Glance
The area of a regular pentagon looks about twice as a big as the pentangle star drawn within it. Is it?