Opposite Vertices printable sheet - squares
Opposite Vertices printable sheet - rhombuses
Printable 10mm Dotty Grid

Charlie has been exploring squares with vertices drawn on the points of a square dotty grid.
Unfortunately, he rubbed out some of his work and only left behind one side of each square.
 

 

Can you recreate the squares he drew?
Is there more than one possibility?

Could any line joining two points be the side of a square whose vertices lie on grid points?
How can you be sure?

 
Alison has been drawing squares and their diagonals. Here are some of the diagonals she drew:

 

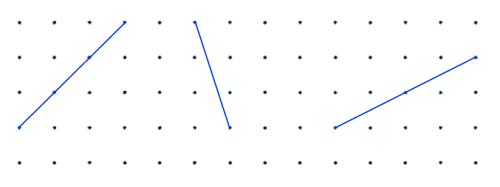
Can you recreate the squares she drew from her diagonals?
Is there more than one possibility?

Can you find a method to draw a square when you are just given the diagonal?
 
Could any line joining two points be the diagonal of a square whose vertices lie on grid points?
 
Can you find a way to help Alison decide whether a given line could be the diagonal of such a square?

 
Charlie and Alison played around with rhombuses next.
 
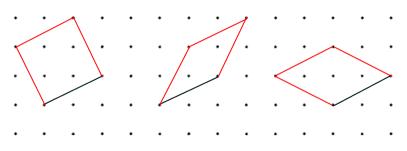
Charlie said "Whenever I join two points to make a line, I can use my line as a side of several different rhombuses".

 

 
Alison said "When I draw a rhombus, it shares its diagonal with infinitely many other rhombuses."

 

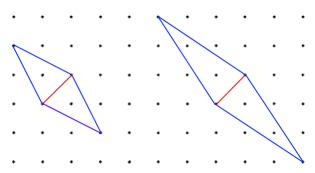
Do you agree with her?

Not all lines can be the diagonal of a rhombus. Is there a quick way to decide which lines could be the diagonal of a rhombus?