Copyright © University of Cambridge. All rights reserved.
'Inky Cube' printed from https://nrich.maths.org/
Show menu
Demi, Hannah, Izobel, Celia, Joseph and Michael from All Saints C of E Junior School sent us their solution to this challenge. They said:
First we divided the grid into 12 compartments each of 9 squares (3x3).Then we covered a large dice in paper and stuck it with sellotape.
Next we drew the top left corner pattern onto a side of the dice.
Then we rolled it down once, then drew on that pattern.
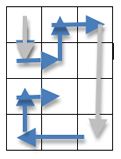
After doing lots of trial and error we found out a route:
We started at the top left corner and then went down 1 space, right 1, and then up 1.
Next we went to the right and down 3.
Then we went left 2, up 1 and 1 to the right! (the finishing point!)
I've drawn a rough sketch to show the route they describe:
They also sent in a net of the cube:

Niharika from Leicester High Schools for Girls told us:
I saw the cube turn in the air. It was hard but I enjoyed it.Mathematicians might call that 'visualising'. Niharika sent in another solution which is the reverse of the route above.
Niharika also tackled the second part of the challenge which involved a cube with coloured squares painted on it. Firstly, she labelled the grid:

She then went on to describe the route:
(1, 1) --- (2, 1) --- (3, 1) --- (3, 2) --- (2, 2) --- (2, 3) --- (3, 3) --- (3, 4) --- (2, 4) --- (1, 4) --- (1, 3) --- (1, 2)Niharika explained that she thought carefully about the symmetry of each of the faces and how an odd or even number of 'tips' might affect each face. Fantastic!
Will the reverse of Niharika's route work too, do you think?