Attractive Rotations : nrich.maths.org

'Attractive Rotations' printed from http://nrich.maths.org/

Show menu

Take a look at the image below. How do you think it was created?

Did you notice any symmetry in the image?
Does this help you to imagine how the image was made?

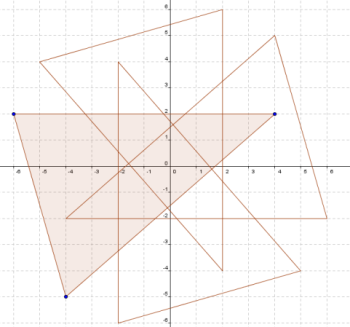
Here is a diagram which shows how we created the image. We started with a triangle (shaded) and then used the coordinate grid to help us to rotate it through multiples of $90^{\circ}$ around the point $(0,0)$.

Create some images of your own by rotating a shape through multiples of $90^{\circ}$.

You might like to start with a triangle as we did, or you might want to use other shapes.

How can you use a coordinate grid to help you to rotate each point around $(0,0)$?

What is the relationship between the coordinates of the points as they rotate through multiples of $90^{\circ}$?

Here are some more ideas to explore:

Can you use an isometric grid to rotate a shape through multiples of $60^{\circ}$?

Try creating some images based on other rotations, such as $30^{\circ}$ or $72^{\circ}$ or... (you will need to use a protractor for these). What do you notice about the rotational symmetry of your images?

What is the rotational symmetry of your final image if you rotate through multiples of $80^{\circ}$ or $135^{\circ}$? Can you explain why?

Here is the kind of image you could try to create:

Send us pictures of your rotation patterns along with your interesting mathematical discoveries.