Copyright © University of Cambridge. All rights reserved.
'Sorting the Numbers' printed from https://nrich.maths.org/
Show menu
Why do this problem?
This problem offers learners the chance to explore their own questions, conjecture and possibly prove results. They will also be engaged in lots of calculating.
This activity lends itself to collaborative working, both for children who are inexperienced at working in a group and children who are used to working in this way. By working together on this problem, the task is shared and therefore becomes more manageable than if working alone.
Many NRICH tasks have been designed with group work in mind. Here we have gathered together a collection of short articles that outline the merits of collaborative work, together with examples of teachers' classroom practice.
Possible approach
This is an ideal problem for learners to tackle in groups of four. Allocating these clear roles (Word, pdf) can help the group to work in a purposeful way - success on
this task could be measured by how effectively members of the group work together as well as by their final solution. This version of the roles has been adapted for primary children.
Introduce the four group roles to the class. It may be appropriate, if this is the first time the class has worked in this way, to allocate particular roles to particular children. If the class works in roles over a series of lessons, it is desirable to make sure everyone experiences each role over time.
For suggestions of team-building maths tasks for use with classes unfamiliar with group work, take a look at this article and the accompanying resources.
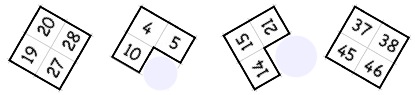
You could give each group a copy of the two jigsaws and invite them to split into two pairs to start with, each pair working on one jigsaw. Once the jigsaws are complete, give out the blank grids and explain the rest of the task. It might be useful for each group to have a large sheet of paper on which they can record patterns and relationships they have noticed along with any explanations they have.
In the plenary, the whole class can share their findings so far. The discussion may reveal some patterns that can't be explained yet. If you post these up onto a wall in the classroom, then children can continue to work on the task during the coming week or even at home.
Key questions
If your focus is effective group work, this list of skills may be helpful (Word, pdf). Ask learners to identify which skills they demonstrated, and which
skills they need to develop further.
If your focus is mathematical, these prompts might be useful:
What ideas have you come up with and will you be able to share it with the whole class?
What patterns or relationships have you come across?
Why are these relationships occurring?
Possible extension
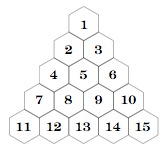
You can try a triangular arrangement so we might have a fifteen triangle placed on a thirty-six triangle:
 |
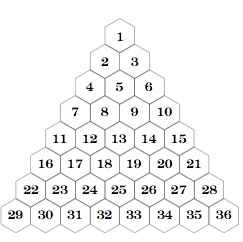 |
You can print these triangles here.
Possible support
By working in groups with clearly assigned roles we are encouraging children to take responsibility for ensuring that everyone understands before the group moves on.