The Numbers Give the Design

'The Numbers Give the Design' printed from https://nrich.maths.org/

Show menu

The Numbers Give the Design

How about making designs like the ones above?

It's just a matter of getting a group of numbers together that repeat and then using a simple drawing rule, then colouring the pattern in.

A good way to start is to take a number sequence that you like, for example square numbers or the $3$ times table.
Just keep the ones (units) of those numbers, for example $1, 4, 9, 6, 5, 6, 9, 4, 1, 0, 1, 4$ etc. or $3, 6, 9, 2, 5, 8, 1, 4, 7, 0, 3, 6$ etc.
You may notice that with these, and perhaps your own sequences, they go to a $0$ and then repeat.

For this challenge, you just need the numbers that go as far as just before the zero, for example $1, 4, 9, 6, 5, 6, 4, 1$ or $3, 6, 9, 2, 5, 8, 1, 4, 7$.

Now to draw ...

Using squared paper and starting somewhere in the middle, take each of the numbers in turn to tell you how long to draw the line and turn a right angle to the left after you've drawn each line.

This may help you to see what to do, using the example of square numbers and starting with the red $1$. I've coloured each new line with a different colour:

After the final $1$ you start again as shown below:

and so on until you get back to the beginning.
Some squences that you choose may not come back to the start but just keep stepping away!

So now it's your turn ...
Choose your sequence.
Pick out the ones (units) until you find it repeating.
Draw the lines carefully on squared paper turning in the same direction each time by a right angle.
See what you get and colour it in if you like.

You may like to change a rule or two after a while. (For example, you could change the turn to $60^\circ$ instead of $90^\circ$.)

Please send us your pictures.

Why do this problem?

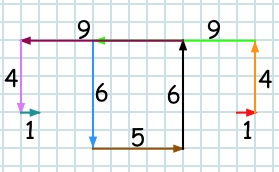
This activity engages the pupils in a simple geometric construction that has the potential to generate enthralling designs. Children who use Logo or control robots like Roamer or Pixie might like to explore in a different way without the need for geometric drawings. The task offers the learners the opportunity to vary their input, observe the effects, and begin to make predictions and perhaps generalisations. You could think of the sequence of instructions both as a sequence of actions (turn $90^\circ$ and then go forward the specified amount) and as a compound action, namely as a single action that is to be repeated over and over.

Possible approach

Show the designs and ask the children what it is that they see or what strikes them about the images.

Reveal how they are constructed so simply from lines and turning right angles. Discussion can then focus on the choice of numbers that repeat themselves. What sequences might they like to try?

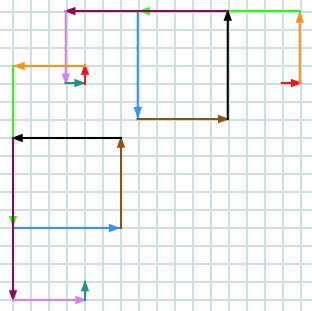
Once everyone has tried out a number of different sequences, you could encourage children to 'tweak' one of their sequences. Can they predict what difference their 'tweaking' will make to their design? They could then test their ideas.

The resulting designs would make a lovely display and children could be involved in writing the description of how the patterns were produced. It may also be possible for learners to make some general statements about the designs.

Key questions

What can you see?

Tell me about your sequence of numbers.

Which parts do you like/dislike?

What could you change?

Can you make any predictions about your new pattern before you draw it?

Possible extension

Pupils can select a random set of numbers to use and see their effect, then adjust the numbers in a particular way for the next design they try.

Possible support

Some pupils may need some help with the drawing of straight lines accurately. Those that want to pursue turning by different amounts might find isometric paper helpful.