You may also like
Doodles
Draw a 'doodle' - a closed intersecting curve drawn without taking pencil from paper. What can you prove about the intersections?
Russian Cubes
I want some cubes painted with three blue faces and three red faces. How many different cubes can be painted like that?
Picture Story
Can you see how this picture illustrates the formula for the sum of the first six cube numbers?
Age 14 to 16
Challenge Level
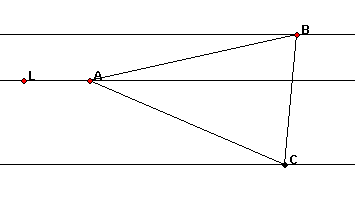
This is another tough nut mind bender, and we have to give a proof of existence. The conjecture is that, given any set of three parallel lines, there always exists an equilateral triangle with one of its vertices on each of the lines. The trouble with this sort of mathematics is that there are infinitely many possible cases. It means nothing that the conjecture holds true in every case we test because it might still break down in a case we have not tried. So what can be done? Playing with the dynamic diagram suggests that the length of BC changes - how does it change?
NRICH is part of the family of activities in the Millennium Mathematics Project.