Copyright © University of Cambridge. All rights reserved.
'The History of Negative Numbers' printed from https://nrich.maths.org/
Show menu
|
Although the first set of rules for dealing with negative
numbers was stated in the 7th century by the Indian mathematician
Brahmagupta, it is surprising that in 1758 the British
mathematician Francis Maseres was claiming that negative
numbers
"... darken the very whole
doctrines of the equations and make dark of the things which are in
their nature excessively obvious and simple" .
Maseres and his contemporary, William Friend took the view
that negative numbers did not exist. However, other mathematicians
around the same time had decided that negative numbers could be
used as long as they had been eliminated during the calculations
where they appeared.
|
 |
It was not until the 19th century when British mathematicians like De Morgan, Peacock, and others, began to investigate the 'laws of arithmetic' in terms of logical definitions that the problem of negative numbers was finally sorted out.
However, there were references to negative numbers far earlier...
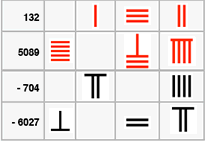 |
In 200 BCE the Chinese number rod system (see note1 below) represented positive numbers in Red and Negative numbers in black. An article describing this system can be found here . These were used for commercial and tax calculations where the black cancelled out the red. The amount sold was positive (because of receiving money) and the amount spent in purchasing something was negative (because of paying out); so a money balance was positive, and a deficit negative. |
The concept also appeared in Astronomy where the ideas of
'strong' and 'weak' were used for approximating a number from above
or below. For example approaching 5 from above means for example,
starting with 5.2 you can find better approximations 5.1, 5.05,
5.025. Thus 5.025 was called a 'strong' approximation and a number
like 4.9 'weak'. So 'strong' numbers were called positive and
'weak' numbers negative
In India , negative numbers did not appear until about 620 CE in the work of Brahmagupta (598 - 670) who used the ideas of 'fortunes' and 'debts' for positive and negative. By this time a system based on place-value was established in India, with zero being used in the Indian number sytem. Brahmagupta used a special sign for negatives and stated the rules for dealing with positive and negative quantities as follows:
|
A debt minus
zero is a debt.
A fortune minus
zero is a fortune.
Zero minus zero
is a zero.
A debt
subtracted from zero is a fortune.
A fortune
subtracted from zero is a debt.
The product of
zero multiplied by a debt or fortune is zero.
The product of
zero multiplied by zero is zero.
The product or
quotient of two fortunes is one fortune.
The product or
quotient of two debts is one fortune.
The product or
quotient of a debt and a fortune is a debt.
The product or quotient of a fortune and a
debt is a debt.
|
 |
The conflict between geometry and algebra
The ancient Greeks did
not really address the problem of negative numbers, because their
mathematics was founded on geometrical ideas. Lengths, areas, and
volumes resulting from geometrical constructions necessarily all
had to be positive. Their proofs consisted of logical arguments
based on the idea of magnitude. Magnitudes were represented by a
line or an area, and not by a number (like 4.3 metres or 26.5 cubic
centimetres). In this way they could deal with 'awkward' numbers
like square roots by representing them as a line. For example, you
can draw the diagonal of a square without having to measure it (see
note 2 below).
About 300 CE, the Alexandrian mathematician Diophantus (200 - c.284 CE) wrote his Arithmetica , a collection of problems where he developed a series of symbols to represent the 'unknown' in a problem, and powers of numbers. He dealt with what we now call linear and quadratic equations. In one problem Diophantus wrote the equivalent of 4 = 4x + 20 which would give a negative result, and he called this result 'absurd'.
In the 9th century in Baghdad Al - Khwarizmi (c.780 - c.850 CE) presented six standard forms for linear or quadratic equations and produced solutions using algebraic methods and geometrical diagrams. In his algebraic methodshe acknowledged that he derived ideas from the work of Brahmagupta and therefore was happy with the notion of negative numbers. However, his geometrical models (based on the work of Greek mathematicians) persuaded him that negative results were meaningless (how can you have a negative square?). In a separate treatise on the laws of inheritance, Al-Khwarizmi represents negative quantities as debts.
In the 10th century Abul -Wafa (940-998 CE) used negative numbers to represent a debt in his work on 'what is necessary from the science of arithmetic for scribes and businessmen'?. This seems to be the only place where negative numbers have been found in medieval Arabic mathematics. Abul-Wafa gives a general rule and gives a special case where subtraction of 5 from 3 gives a "debt" of 2. He then multiples this by 10 to obtain a "debt" of 20, which when added to a 'fortune' of 35 gives 15.
In the 12th century Al - Samawal (1130 - 1180) had produced an algebra where he stated that:
- if we subtract a positive number from an 'empty power', the same negative number remains,
- if we subtract the negative number from an 'empty power', the same positive number remains,
- the product of a negative number by a positive number is negative, and by a negative number is positive.
Negative numbers did not begin to appear in Europe until the
15th century when scholars began to study and translate the ancient
texts that had been recovered from Islamic and Byzantine sources.
This began a process of building on ideas that had gone before, and
the major spur to the development in mathematics was the problem of
solving quadratic and cubic equations.
As we have seen, practical applications of mathematics often
motivate new ideas and the negative number concept was kept alive
as a useful device by the Franciscan friar Luca Pacioli (1445 -
1517) in his Summa
published in 1494, where he is credited with inventing double entry
book-keeping.
Solving equations
The story of the solution of equations begins in Italy in the 16th century (see note 3 below). This story is full of intrigue and deception because methods of solution were kept secret. The issue which caused most consternation at the time was the meaning of $\sqrt{-1}$. In fact, Cardano (1501 - 1576) in his Ars Magna of 1545 had to solve a problem where $\sqrt{-15}$ appeared.
Cardano found a sensible answer (see note 4 below) by working through the algorithm, but he called these numbers 'ficticious' because not only did they disappear during the calculation, but they did not seem to have any real meaning. However, by 1572, the Italian engineer, Bombelli (1526 - 1572) had provided the correct rules for working with these 'imaginary' numbers(see note 5 below).In the 17th and 18th century, while they might not have been
comfortable with their 'meaning' many mathematicians were routinely
working with negative and imaginary numbers in the theory of
equations and in the development of the calculus.
The English mathematician, John Wallis (1616 - 1703) is credited with giving some meaning to negative numbers by inventing the number line, and in the early 18th century a controversy ensued between Leibniz, Johan Bernoulli, Euler and d'Alembert about whether $\log (-x)$ was the same as Log(x).

By the beginning of the 19th century Caspar Wessel (1745 - 1818) and Jean Argand (1768 - 1822) had produced different mathematical representations of 'imaginary'numbers, and around the same time Augustus De Morgan (1806 - 1871), George Peacock (1791 - 1858) William Hamilton (1805 - 1865) and others began to work on the 'logic'of arithmetic and algebra and a clearer definition of negative numbers, imaginary quantities, and the nature of the operations on them began to emerge.
Negative numbers and imaginaries are now built into the
mathematical models of the physical world of science, engineering
and the commercial world.
There are many applications of negative numbers today in
banking, commodity markets, electrical engineering, and anywhere we
use a frame of reference as in coordinate geometry, or relativity
theory.
Pedagogical Note:
It seems that the problems that people had (and now have - see the
Lottery incident ) in understanding the use of negative numbers
concerns:
- the difference between the operation of subtraction and the object (a negative number), since the same sign is used for both
- the language involved like 'minus minus 3' as opposed to 'subtract negative 3'
- separating the physical model or analogy (be it profit/loss or rise/fall in temperature or rotation/direction in the plane) from the rules of operating on the entities.
References
English Mathematicians
Francis Maseres (1731 - 1824)
A dissertation on the use of the negative sign in algebra. (1758)
Fellow of Clare College Cambridge and Fellow of the Royal Society
William Frend
Principles of Algebra (1796)
Printed by J. Davis, for G. G. and J. Robinson, Paternoster Row
Other Sources
Berggen, J.L. (1986) Episodes in the Mathematics of Mediaeval Islam . Springer-Verlag N.Y. andBerlin.
Menninger, K. (1969) Number Words and Number Symbols . M.I.T. Press Cambridge, Mass. andLondon.
Schubring, G. (2005) Conflicts Between Generalization, Rigor, and Intuition: Number Concepts Underlying the Development of Analysis in 17 - 19th Century France and Germany . Springer-Verlag N.Y.
Ifrah, G. (1998) The Universal History of Numbers . Harvill Press, London.
Li Yan and Du Shiran (Tr. Crossley, J.N and Lun A. W. ) (1987) Chinese Mathematics: a Concise History . O.U.P. Oxford.
Web References
Mactutor at St Andrews University http://www-history.mcs.st-and.ac.uk/history/ .
Notes
- The counting rod system was certainly in operation in the period (475 - 221 BCE) - called the period of the 'Warring States' [Yan andShiran 1987, 7/8])
- In our notation, $\sqrt{2}$ and $\sqrt{5}$ occurred when finding the diagonal of a square or constructing the Golden Section.
- The period from Pacioli (1494) to Descartes (1637), a period of about 150 years brings the solution of equations to a stage where they could be understood by school pupils today.
- In modern notation, Cardano's multiplication was $(5-\sqrt{-15} )(5+ \sqrt{-15} )$, and applying the rule for brackets this becomes $25 - -15 = 40$.
- Even though mathematicians did not find a suitable representation for negative numbers, it did not prevent them from following the ordinary rules of arithmetic and developing rules for the imaginary numbers as well. This is where the beauty of mathematical invention is not limited by the 'real' world.