While it may be tempting, and fun, to simply try to do the puzzle as it for a while, there is a rather nice way of simplifying the problem.

By joining up each of the squares that are connected by a knights move, we can reduce the problem down to a graph, where the knights can move along connected nodes.

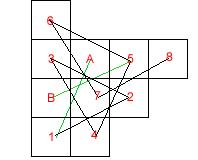
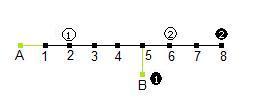
The graph turns out to be rather simple! All of the squares end up on a single line, with the single square 'B' branching off.

Clearly, by moving the pieces along one node at a time, the only place where any swapping can happen is at B. The quickest way would be to swap W1 and B1 , and swap W2 and B2 (otherwise there would be even more swapping. There are two ways of doing this:

Swapping W1 and B1, then W2 and B2: 

• W2: 6 to 7
• W1: 2 to 6
• B1: B to 2
• W1: 6 to 3 (we've now swapped W1 and B1, making room for the next swap)
• W2: 7 to B
• B2: 8 to 4
• W2: B to 8
• B2: 4 to 6.
• W1: 3 to B. Done! 28 moves

Swapping W2 and B2, then W1 and B1:

• B1: B to 3
• W2: 6 to B
• B2: 8 to 4
• W2: B to 8
• B2: 4 to 7 (we've swapped W2 and B2, making room for the next swap)
• B1: 3 to 6
• W1: 2 to B
• B1: 6 to 2 (we've now swapped W1 and B1)
• B2: 7 to 6. Done! 28 moves

So the minimum number of moves is 28.