Copyright © University of Cambridge. All rights reserved.
'How Does Your Function Grow?' printed from https://nrich.maths.org/
Show menu
Here are two solutions, one from Simon from Elizabeth College, Guernsey and one from Andrei from Tudor Vianu National College, Bucharest, Romania. First Simon's solution.
The functions are: $$\eqalign { A(n) &= \log(100n) \cr B(n) &= n^{100} \cr C(n) &= 100^n \cr D(n) &= n! .}$$ Firstly I looked at Archimedes' choice, the logarithmic function. $$A(n) = \log(100n) = \log 100 + \log n.$$ I knew that when $n$ gets large $\log 100$ would become irrelevant. This meant that only $\log n$ would be important, and $\log n < n$ when $n > 1$. So $A(n)$ will be less than $n$ for large $n$. We find $n = \log(100)+ \log n$ for $n = 6.472775$ approximately and so $A(n) < n$ for all values of $n> 6.5$.\par The next task was establish whether $B(n)$ or $C(n)$ was greater for large numbers. I was certain of one thing: $B(n) = C(n) = 100^{100}$ for $n=100$.
Firstly I knew that $100^n$ would have $2n+1$ digits. I then established, where $x$ is the number of digits in $n$, that $n^{100}$ would have between $100(x-1)+1$ and $100x$ digits. So $C(n) = 100^n$ is the larger function for $n> 100$.
Therefore, so far, $C(n)$ is the largest function for large values of $n$.
The next task was to compare it to $D(n)$ or factorial $n$.
Using Stirling's formula: $$D(n) = n! = \sqrt{2\pi n} ({n\over e})^n.$$ As $n$ is a large positive number, $\sqrt {2\pi n}$ will be greater than 1. Therefore when ${n\over e}$ is greater than 100, $D(n) > C(n)$. The 'change over point' occurs for $n$ just less than $n = 100e$, that is $ n \approx 270$.
Andrei considered the natural logarithms of the functions and plotted their graphs. For the factorial n function Andrei used Stirling's Approximation which is valid for large n.
I approximated the function for factorial n further by
ignoring the term $\sqrt{2\pi n}$. $$\eqalign{ A(x)&= \log (n)
+ \log(100) \cr \log(B(n)) &= 100 \log(n)\cr \log C(n) &= n
\log(100) \cr \log D(n)&\approx n\log(n) - n }.$$ I know that
$log(n)< n$ for the whole domain of definition of the
logarithmic function, and I see that $A$ is the smallest. I have to
compare the other functions. As $ \log(100)\approx 4.60$, so:
$$\eqalign { \log(B) &= 100 \log(n) \cr \log(C)&\approx
4.6n \cr \log(D) &\approx n (\log(n) -1).}$$ In the limit for
large $n$, $$ \lim_{n\to \infty}{\log n\over n}\to 0$$ and so
$B< C$.
For large $n$ we can neglect 1 in respect to $\log(n)$ in the
approximate formula for $\log(D)$ and, as $4.6 < \log (n)$ we
have $D> C> B> A$.
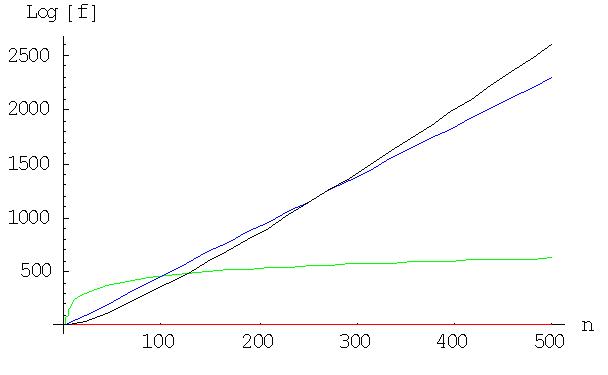
Here in the diagram, $A(x)$ is represented in red, $B(x)$ in
green, $C(x)$ in blue and $D(x)$ in black. It can be observed that
for large $n$ (here $n> 300$) the order of the magnitude of the
functions is $D> C> B> A$.