Nick Lord says that this problem is immediately enticing for students (and for him) and there are many possible approaches to explore and compare.

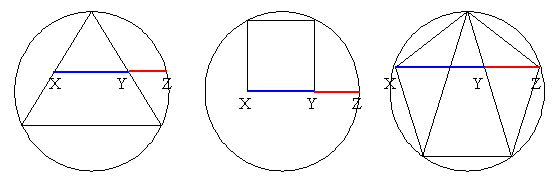
In the equilateral triangle inscribed in the circle, $X$ and $Y$ are the midpoints of the edges. Find the ratio${XZ\over XY}$.

The square sits on a diameter of the circle. Find the ratio ${XZ\over XY}$.

The regular pentagon is inscribed in the circle. Find the ratio ${XZ\over XY}$.

See also the problem Gold Again.